We started with a 30 minute assessment pre-test that is not for a grade. After that we reviewed the rules for working with fractions.
Addition. To add fractions, they need a common denominator (bottom). Once you have a common denominator, just add the numerators (tops). We did these examples:
Multiplication. I like to say that “fractions play nice with multiplication”. To multiply fractions, just multiply the tops and multiply the bottoms.
Division. Division is just multiplication by the reciprocal. You might have learned this as “keep-change-flip” or as “flip-and-multiply”. We did these examples:
Today we reviewed order of operations and how to solve algebraic equations that don’t require factoring. You might have learned the acronym
to remember order of operations. Another acronym is
Algebra notation can be helpful. The notation for multiplication or and division or puts numbers close together. Numbers being added or subtracted are more spread out: . This is deliberate and it can help you remember that numbers being multiplied/divided are more tightly bound together and so those operations come before addition/subtraction.
After reviewing order of operations, we talked about:
The Most Important Rule of Algebra. You can do whatever you want to an equation, as long as you do it to both sides!
More specifically, you can perform any algebraic operation to the expression on the left side of the equals sign as long as you also do the same operation to the right side expression. Caution: Make sure you perform the operation to everything on both sides!
Solve the following expression for :
Solve (https://youtu.be/r95Yh7dMVVc)
We also talked about these two examples.
Simplify
Explain why
We started by talking about Homework 1. When you multiply & divide fractions, look for opportunities to cancel factors whenever possible:
We reviewed these techniques:
Distributing
Factoring out common factors from terms.
Canceling common factors in fractions.
Collecting like terms. The coefficient keeps track of how many terms have been added together.
Expand .
Factor out all common factors from .
Solve .
Simplify . (https://youtu.be/lBQmy1IMko8)
We started by reviewing some of the common mistakes that came up in the last homework. There were two that are worth mentioning.
If you multiply both sides of an equation by a number, make sure you distribute that number to every term!
When you take square roots, there are two answers, a positive one and a negative one.
We reviewed these techniques (which are opposites of each other).
Factoring quadratic polynomials.
FOIL-ing (First-Outside-Inside-Last).
Expand . (https://youtu.be/ZMLFfTX615w)
Solve . (https://youtu.be/2ZzuZvz33X0)
We also talked about the AC-method and factoring by grouping.
Factor . (https://youtu.be/u1SAo2GiX8A)
How would you factor ? Is it easier or harder than the last problem?
Today we talked about graphing equations, and we focused on two important special cases: lines and parabolas.
Equations for Line
Slope-intercept form:
Point-slope form:
where is the slope, is the y-intercept and are the coordinates of any point on the line.
Find an equation for the line that passes through and in slope-intercept and point-slope form. (https://youtu.be/lzqTD0JWwhY?t=174)
Graph the line through with a slope of . (https://youtu.be/5mgH-_5UJ54)
Quadratic Polynomials
The graph of is a parabola.
The roots are where the graph crosses the -axis.
If you can’t factor, then you can find the roots using the quadratic formula
The vertex is where the parabola reaches its highest (or lowest) point. It is located at
What are the x-values of the roots and vertex for the parabola ? Use those to help sketch a graph of the parabola.
A local elementary school wants to make a rectangular flower garden along the side of the school building. One side of the garden will the be along the wall of the school, but the other three sides will be fenced off. If you have 60 feet of fencing material, what is the largest area possible for the flower garden?
We didn’t have time for this last example, but there are a couple of problems on homework 5 that use this idea:
We started by going over questions about Homework 5 and some of the common mistakes on Homework 4. In particular we talked about the fact that a fraction is zero when its top is zero. A fraction is undefined if the bottom is zero, and we talked about why that is..
After that, we talked about function notation and graphs. We did the following examples.
We also defined the domain and range of a function. Then we looked at different ways to express functions. For example, we had these two examples:
The volume of a sphere: .
The function to convert Celsius to Fahrenheit: .
We also talked about inverse functions
Find the inverse of and explain what it does in words.
Find the inverse of . (see: https://youtu.be/W84lObmOp8M)
Finally we looked at using the graph of a function to answer questions like the following:
Today we had the first midterm exam.
Today we went over the midterm exam. We also talked about the
This week we talked about using algebra to solve inequalities.
Function Crossing Rule
For two functions defined using the usual operations (,,,), the function which is greater can only change at an -value where the graphs cross (are equal) or where one is undefined (a bad point).
Therefore you can solve complicated inequalities with these two steps:
We used this method to solve these examples.
(Video solution: https://youtu.be/D1cKk48kz-E)
(Example video: https://youtu.be/a10EuIFcphk)
We had the second midterm exam this week.
This week was about working with exponents.
Understanding Exponents
Powers represent repeated multiplication.
Negative powers represent reciprocals.
Fraction powers represent roots.
From these basic ideas, you can work out all of the other exponent rules.
|
Powers Count Repeated Factors Add powers of factors when you multiply. Subtract powers when you divide. |
Powers Distribute to Factors Powers do not distribute to terms. |
|
Power of a Power |
Zero Power |
We simplified these examples in class:
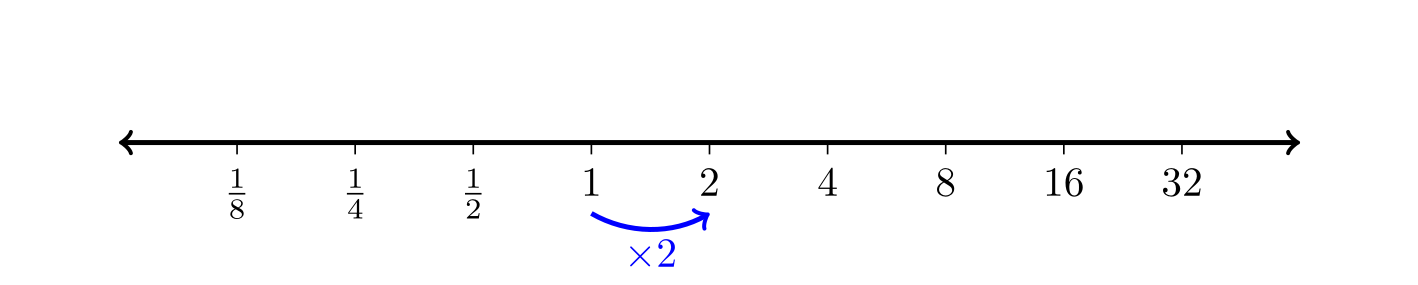
Today we introduced logarithms. We started by talking about logarithmic scales, which are number lines where the numbers are spaced by multiplication instead of addition.

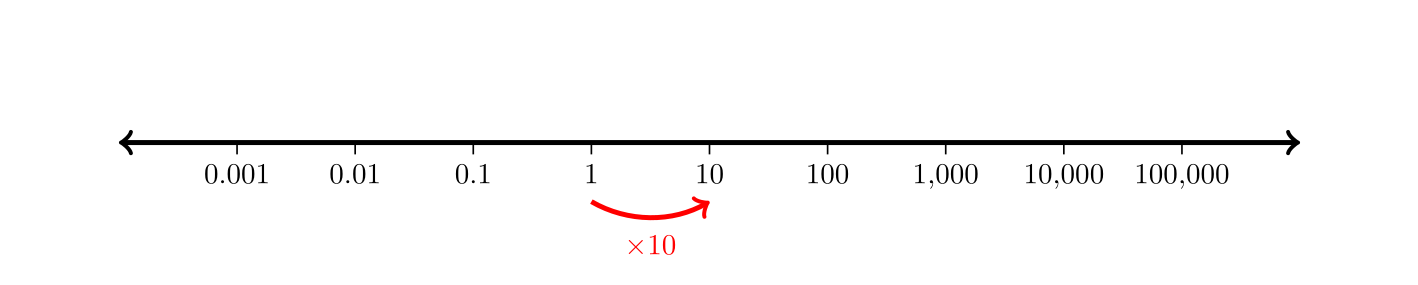
Logarithmic scales help understand the logarithm function.
What are Logarithms?
The logarithm function can be understood two ways:
equals the number of steps is away from 1 on a (base-b) log-scale.
equals the power of b needed to get .
Logarithms are useful because they convert difficult multiplication/division problems into easier addition/subtraction problems. They also convert exponential patterns into linear patterns.
Properties of Logarithms
The most important base for exponential and logarithmic functions in calculus is the number . This is the natural base for the logarithm and exponential function for reasons that we’ll see later when we talk about derivatives. We write to denote the base-e logarithm.
One of the most important applications of logarithms is that they let you solve equations with variables in the exponent.
Solve .
Solve (video)
We started by going over some problems from homework 10. Then we talked about these examples.
Where do the lines and intersect?
What are the solutions of the system of equations and ? (https://youtu.be/swFohliPgmQ)
Solve . (https://youtu.be/R443Db-wJ5o)
After that, we spent the last 20 minutes of class on this practice final exam.
The final exam is Monday, Dec 8. at 2:30pm (our regular class time and room).