| Day | Section | Topic |
|---|---|---|
| Wed, Jan 17 | 1.1 | Review of functions |
| Thu, Jan 18 | 1.2 | Basic classes of functions |
| Fri, Jan 19 | 1.2 | Basic classes of functions - con’d |
Today we reviewed functions and function notation. We talked about how looks like multiplied by , but it really means something completely different! We also talked about the following important functions (and their graphs) that you should have memorized:
Linear functions .
The square function .
The positive square-root function .
The reciprocal function .
The 1-dimensional distance function .
We reviewed the definitions of domain, range, and function composition. We did the following examples in class.
Let and . Find the domain of . (https://youtu.be/PNzHrPebKOw)
Two poles are connected by a wire that also connects to the ground between the poles. Find a formula for the length of the wire as a function of and determine the domain.
We didn’t have time for this exercise, but it is also a good example of how to construct a function.
Today we started with the wire between two poles example from yesterday. Then we focused on linear functions. We reviewed slope-intercept form and did the following examples in class.
Find the formula to convert Celsius temperatures to Fahrenheit.
Find a formula for the line through and . (https://youtu.be/LtpXvUCrgrM)
As of 2023-24, the US Income Tax brackets for individuals earning up to $95,375 are:
| Taxable Income | Rate |
|---|---|
| $0 to $11,000 | 10% |
| $11,000 to $44,725 | 12% |
| $44,725 to $99,375 | 22% |
Here is another good example that we didn’t do in class:
Today we talked about polynomial functions and equations. We briefly reviewed how to factor polynomials and we solved the following problems.
In the last example, you should get to . Unfortunately there aren’t integer factors of that add up to . So you need to use the quadratic formula to find all of the solutions. You do not need to memorize the quadratic formula (it will be on the formula sheet on exams and you can look it up when you are doing your homework if needed).
| Day | Section | Topic |
|---|---|---|
| Mon, Jan 22 | 1.3 | Trigonometric functions |
| Wed, Jan 24 | 1.3 | Trigonometric functions |
| Thu, Jan 25 | Review | |
| Fri, Jan 26 | 2.1 | A preview of calculus |
Today we did a review of some basic trigonometry. We talked about the things you should memorize which include:
We did the following exercises.
Convert radians to degrees. (https://youtu.be/z0-1gBy1ykE)
Convert to radians. (https://youtu.be/O3jvUZ8wvZs)
Find the values of and for the angle shown below.
Find . Hint: use the formula sheet.
Find (https://youtu.be/KaS3P1a7GE8)
Find
Find all solutions to .
Solve . (https://youtu.be/j7c2I_fwamc)
A 1000 meter long driveway in the mountains has a grade. How much elevation do you gain when you drive up the driveway?
Today we looked at some more trigonometry examples. We did the following:
The radius of the Earth is about 4000 miles. Farmville has a Latitude of 37.3. How far is Farmville from the the equator?
A lighthouse is 25 meters above sea level. A boat measures the angle of elevation of the light to be . How far is the boat away from the base of the lighthouse as a function of ?
Prove the Law of Sines (for any triangle, the following formula is true): (https://youtu.be/APNkWrD-U1k)

Simplify . (https://youtu.be/-s44LcIPaPU)
Simplify as much as possible. (https://youtu.be/0QuB4HOI3J8)
Find all solutions of in the interval .
Find all solutions of on . (https://youtu.be/vVR91JqJEMQ)
Today we went over homework 2. We also did the following additional exercise in class.
Today we started talking about limits. We began with this example:
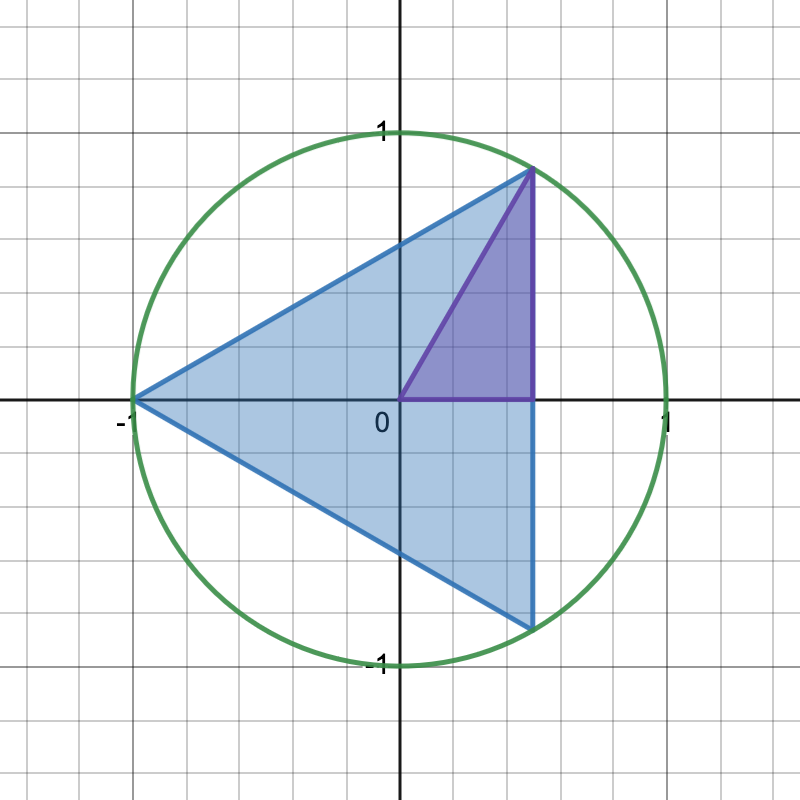
What is the area of a regular -gon inscribed in the unit circle?
What happens to the area as the number of sides gets bigger and bigger?
A sequence is a special kind of function which has domain equal to the natural numbers . We say that an interval eventually contains a sequence if there is a number such that for all . If every interval that contains eventually contains , then we say that converges to the limit . This can be written as:
We finished by looking at another example of a limit. Galileo was the first person to observe that the distance traveled by an object that is dropped from a great height is roughly meters (when is the time in seconds after the object was dropped). The average velocity of a falling object is
These two examples, the area of a circle and the instantaneous velocity of a falling object, are both limits. Next week, we’ll look at how to work systematically with limits.
| Day | Section | Topic |
|---|---|---|
| Mon, Jan 29 | 2.2 | Limit of a function |
| Wed, Jan 31 | 2.3 | Limit laws |
| Thu, Feb 1 | Review | |
| Fri, Feb 2 | 2.4 | Continuity |
Today we defined limits for functions. We say that the limit of as approaches is and write if every sequence that converges to (but never equals ) has .
We looked at two examples on Desmos where a function is not defined but its limit is:
.
.
Both of these are examples of hole discontinuities. We also saw three other common types of discontinuities:
(Pole discontinuity) at .
(Jump discontinuity) .
(Oscillation discontinuity) at .
In all three of these cases, the limit at the point of interest does not exist. But there are also one-sided limits which do exist. For example, the one sided limit as approaches from above is in example 3 is: and the one-sided limit as approaches from below in number 4 is: You mostly just need an intuitive understanding that a limit is the -value that the graph is heading towards, not the actual -value at the point.
We did the following two examples of finding limits graphically:
We finished by talking about another example of a limit:
Today we talked about using algebra to find limits. We did the following examples.
.
Find . (https://youtu.be/bV0RTtywt4g)
At this point, defined continuous functions. A function is continuous at if . Intuitively, a function is continuous if you can draw it without lifting your pencil. Most simple functions (including all linear functions and and ) are continuous at every real number. It turns out that every function constructed from other continuous functions using the operations of addition, subtraction, multiplication, division, powers, and function composition are always continuous at every point in their domains. The only functions you need to worry about are piecewise functions.
Today we went over homework 3.
| Day | Section | Topic |
|---|---|---|
| Mon, Feb 5 | 3.1 | Defining derivatives |
| Wed, Feb 7 | 3.2 | The derivative function |
| Thu, Feb 8 | Review | |
| Fri, Feb 9 | 3.3 | Differentiation rules |
We started by talking about continuity.
We also talked about the intermediate value property of continuous functions. If is continuous on an interval , and is between and , then there is a point between and such that .
Then we introduced the derivative for a function at a point . The derivative is the slope of the tangent line of the function at the point . The actual definition of the derivative is
We calculated some examples.
Find the derivative of at any point .
Find the derivative of at .
What is the derivative of at ? Why doesn’t it exist?
Find the derivative of at . To do this last problem, you need to find . (https://youtu.be/8LJC56j9gHA)
Today we observed that the derivative of is a function that depends on the point where you found the slope of the tangent line. Another way to write the definition of derivative is: We also have two different notations for the derivative function. We’ve already seen . We also use the symbol as a command that literally means “take the derivative of” whatever function comes next. So means the same thing as Another notation that we use frequently is to write to represent the derivative of a function . So if we have a function , then all of these are the same:
We used the definition formula above to find
.
.
We also looked at how the graph of a derivative is related to, but different from, the graph of the original function .
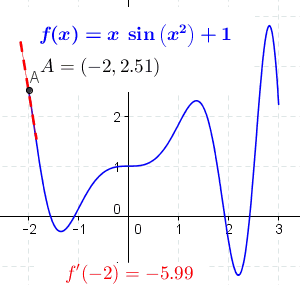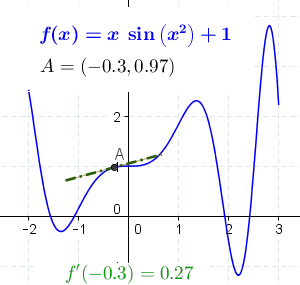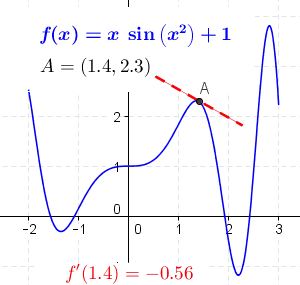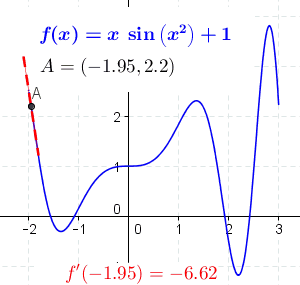
We finished by talking about the two meanings of the derivative.
We looked at this example.
Today we introduced the following derivative rules.
We used these rules to solve the following problems.
Find when . (https://youtu.be/8Sv6CNuNwqo)
Find points on the curve where the tangent is horizontal. (https://youtu.be/KxqKelxk3FA)
Find the derivatives of , , and . Use the exponent rules before you use the power rule.
We also talked about higher derivatives. The second derivative of a function is:
We can also take 3rd, 4th, etc. derivatives and they have similar notation.
| Day | Section | Topic |
|---|---|---|
| Mon, Feb 12 | 3.3 | The product and quotient rules |
| Wed, Feb 14 | 3.4 | Derivatives as rates of change |
| Thu, Feb 15 | Review | |
| Fri, Feb 16 | Midterm 1 |
In class today, we covered these four derivative rules:
We did the following examples.
Let and have values in the following table. Find the derivative of at . (https://youtu.be/SQUSh1LNjIo)
We also gave a proof of the product rule similar to the one in this video.
Today we focused on examples of derivatives and what they mean.
A rock falls from a 100 foot cliff with height where is measured in seconds. What is the velocity of the rock when it hits the ground (i.e., when )? (https://youtu.be/OIo5lfyc8A0)
What is the acceleration of the rock?
(Exercise 3.4.164) A small town in Ohio commissioned an actuarial firm to conduct a study that modeled the rate of change of the town’s population. The study found that the town’s population (measured in thousands of people) can be modeled by the function where is measured in years.
What is and what are its units?
What is and what are its units? What does the second derivative tell us about the population.
A company sells widgets. The amount of widgets they can sell depends on the price in dollars. Suppose that quantity sold is .
What is the total revenue ?
What does the derivative mean?
Let . Find the tangent line at the point . (https://youtu.be/8p7QGLzOynI)
Let . Find the tangent line to when . Where does that tangent line intersect they -axis?
| Day | Section | Topic |
|---|---|---|
| Mon, Feb 19 | 3.5 | Derivatives of trigonometric functions |
| Wed, Feb 21 | 3.6 | The chain rule |
| Thu, Feb 22 | Review | |
| Fri, Feb 23 | 3.6 | The chain rule - con’d |
Today we covered the derivatives of trigonometric functions in more detail. We started with this limit problem.
Then we applied that limit to prove the two fundamental limits of trigonometry
Then we used the angle addition formula for to prove that . Then we solved the following problems.
Find the derivatives of and .
Find the derivative of . (https://youtu.be/tXc8A3VpNOI)
Find the derivative of .
We finished by looking at the graph of . This is a wave that oscillates twice as fast as the regular . So intuitively, its tangent lines should be twice as steep. It turns out that they are because of the chain rule which is a rule for taking the derivative of functions when they are composed together.
Today covered the chain rule in more detail.
.
Compare these two derivatives versus .
We didn’t do this one in class, but it is a good exercise: Use Leibniz notation to find the derivative of . (https://youtu.be/Ur_kdKXnZPo)
Find the derivative of . (https://youtu.be/TlE8bXB53Zw)
Find . (https://youtu.be/S62sK5XoRQo)
Find the equation for the tangent line to the function at the point .
Today we talked about the chain rule some more. We did the following examples.
Find the derivative of . (https://youtu.be/ed5pQoqHXeU)
Suppose that the crime rate in a city is a function of the population . The population is a function of time in years. Suppose that the city’s population is currently 300,000 at . If people per year and crimes per person, then estimate the rate of change in crime this year.
Let be the sine function for angles measured in degrees. So for example, . What is the derivative of ? Hint: .
Find .
| Day | Section | Topic |
|---|---|---|
| Mon, Feb 26 | 3.8 | Implicit differentiation |
| Wed, Feb 28 | 3.8 | Implicit differentiation - con’d |
| Thu, Feb 29 | Review | |
| Fri, Mar 1 | 4.1 | Related rates |
To we introduced implicit equations and implicit differentiation. Implicit equations involving and are sometimes called implicit functions, but they aren’t really functions because one value can correspond to multiple values. But if we act like is a function of and use the chain rule each time we see a in the equation, we can still find the derivative which is still the slope of the tangent line. We started with this example.
Find the slope of the tangent line at the point on the circle defined by .
Find for any point on the parabola .
Find when .
Consider the closed curve defined by the equation Find the coordinates of the two points on the curve where the tangent line is vertical. (https://youtu.be/-jcVn0yCJ6E)
We didn’t get to this last example, except to mention its name, but I’ll mentioned it now, and hopefully get to it next time.
We started with some more examples of implicit differentiation.
Then we introduced an application of implicit differentiation called related rates with the following example. First note that an object moving on the xy-plane has two components of velocity:
If we know one of these velocities, we can use implicit differentiation to find the other.
Today we talked about related rates. We did these examples.
A pebble dropped into a pond makes circular ripples. The radius of the ripples increases at a rate of 1 cm/sec. Find how fast the area is increasing when the radius is 3 cm. (https://youtu.be/kQF9pOqmS0U)
A 10 foot long ladder leans against a wall. Suppose the bottom of the ladder is sliding away from the wall at a rate of 2 ft/sec when the base of the ladder is 6 ft. away from the wall. How fast is the top of the ladder sliding down at that instant? (https://youtu.be/p_QyOi2MbFQ)
A camera is rotating to track a rocket launched vertically from a platform that is 3,000 ft from the camera. If the rocket’s velocity is 1,000 ft/sec, how fast is the camera angle changing (in radians/sec) when the rocket is 4,000 feet up?
Here is one more example that we didn’t have time for in class:
| Day | Section | Topic |
|---|---|---|
| Mon, Mar 4 | 4.2 | Linear approximations |
| Wed, Mar 6 | 4.2 | Differentials |
| Thu, Mar 7 | Review | |
| Fri, Mar 8 | 4.3 | Maxima & minima |
We’ve already talked about tangent lines, but a tangent line at a point on the graph of a function is the best linear approximation function for near (also known as the linearization. It is important enough that I have included this formula on the formula sheet. Sometimes we use to denote this linear approximation function.
Find a linear approximation for the function near , then use it to estimate . (https://youtu.be/u7dhn-hBHzQ)
Find the linearization of at . Use this to estimate . (https://youtu.be/oYSyaM9wB9U)
Find the linearization of at . (https://youtu.be/l8PFsYI3bzw)
Suppose I drive 360 miles, and then need to fill up my car with
gas. If it takes 10.5 gallons, I’d like to estimate how many miles per
gallon my car got on that last tank of gas. So I have to calculate
,
but that is too hard to do without a calculator. Instead, I can use a
linearization of the function
at the point
to try to get a good estimate.
Today we introduced differential notation. For a function and two -values and , we can talk about the change in x and the change in y:
If we use the tangent line at instead of the function to find the change in , then we get what are called differentials:
Intuitively, and are two different notations for the exact same thing. But and are not the same. The differential is the change in using the tangent line while is the change in using the function .
Find the differential of at when (https://youtu.be/4qqNe_hfoz8)
Find the differential of . (https://youtu.be/CGDeNaR0LYk)
Ignoring air resistance, then range of a canonball launched with angle of elevation in a large flat field is .
The (average) radius of the Earth is approximately miles. The radius is actually a little bit lower than that. There is error in the number which can be represented by saying that . If we use the radius to compute the surface area using the formula , how much error might there be in our calculated answer? (https://youtu.be/CGDeNaR0LYk?t=185)
The answer to the last exercise seems big ( square miles). But relative to the surface area of the Earth, it actually isn’t that big. So when working with differentials to estimate measurement error, we often calculate the relative error which is
Today we talked about how to find the absolute maximum and minimum (also known as the global maximum/minimum) of a function on a closed interval . For a continuous function on an interval, there is always an absolute max (and min) and it will always occur at either an endpoint of the interval or at a critical point which is a point where or does not exist.
Find the absolute maximum and minimum of on the interval . (https://youtu.be/ADvCJh9seIY)
Find the absolute maximum and minimum of on the interval . (https://youtu.be/cV1tpeY5mE4)
Find the absolute maximum and minimum of on .
Here is one more example that we did not have time for in class.
| Day | Section | Topic |
|---|---|---|
| Mon, Mar 18 | 4.3 | Maxima & minima - con’d |
| Wed, Mar 20 | 4.4 | The mean value theorem |
| Thu, Mar 21 | Review | |
| Fri, Mar 22 | Midterm 2 |
Extreme Value Theorem. If is a continuous function on a closed, bounded interval , then must have an absolute maximum and an absolute minimum value in that interval.
Give an example of a discontinous function with no absolute max or min on the interval .
Given an example of a continous function with no absolute max or min on the interval .
Find the absolute maximum and minimum of on .
Find the critical x-values of . (https://youtu.be/XJwpmKyaG3A)
Find the absolute max and min for on (okay to use a calculator).
We started with this warm-up problem.
Then we proved some theorems. We started with this theorem:
Rolle’s theorem. If is a continuous function on an interval , and is differentiable on , and , then there must be a point such that and .
To prove Rolle’s theorem, we answered these questions:
How do we know that has an absolute max and an absolute min on ?
What would happen if the absolute max and absolute min both happen at the endpoints? What would that mean about ?
What would happen if either the absolute max or absolute min occurs inside ? What would that mean about the point in where the absolute max or min occurs?
After proving Rolle’s theorem, we introduced the mean value theorem (MVT for short).
Mean value theorem. If is a continuous function on an interval , and is differentiable on , then there must be a point such that and
Intuitively this makes sense. It says that the average rate of change over an interval is equal to the instantaneous rate of change at at least one point inside the interval. We talked about the example of drive 100 miles in just 1 hour on a highway. How can you tell that your car’s speedometer actually hit 100 mph exactly?
We finished by talking about some applications of the MVT.
If for every in , what does the mean value theorem say about and ?
If for every in , what does the mean value theorem say about and when ?
| Day | Section | Topic |
|---|---|---|
| Mon, Mar 25 | 4.5 | Derivatives and the shape of a graph |
| Wed, Mar 27 | 4.5 | Concavity |
| Thu, Mar 28 | Review | |
| Fri, Mar 29 | 4.7 | Applied optimization |
Today we talked about using the first derivative to find the intervals of increase and decrease of a function. We did the following examples.
We started with this example where we found intervals of increase and decrease as well as local max & mins.
Then introduced the notion of concavity. A function is concave down at if is below the tangent line for all near . The function is concave up if is greater than for all close to . It turns out that a function is concave up exactly when the second derivative is positive and concave down when is negative. A point where the concavity changes from positive to negative or vice versa is called an inflection point.
We used the second derivative to find the intervals of concavity (intervals where the function is concave up or concave down) for these functions, and we also found the inflection points.
Today we applied the techniques we’ve learned to solve optimization word problems. We did these examples.
A farmer wants to fence off a rectangular plot of land along the side of a long straight river. He has a total of 2400 feet of fence. How large of and area can he fence off? (https://youtu.be/gt4Qtp0Wxtk)
A cylindrical can must hold 1 liter (1000 cubic centimeters) of oil. What dimensions (height and radius) minimize the surface area of the can? (https://youtu.be/e0Fgyca6WCw) Note: I made a mistake when I solved this in class and forgot a square at one point. Sorry about that!
We also talked about using the first derivatives and the intervals of increase/decrease to double check that a critical point is a max or a min (the first derivative test) and how to check whether a critical point is a max or min by checking the second derivative at that point (the second derivative test).
Here are some other examples that we didn’t have time for today.
A rectangular piece of cardboard is 20 inches by 30 inches. If we cut a square from each corner of the cardboard and fold up the sides to make a box, how big should the squares be in order to maximize the volume? (https://youtu.be/MC0tq6fNRwU and https://youtu.be/cRboY08YG8g)
A cone is made from a circular piece of paper (with radius ) by cutting out a slice and bringing the two sides of the slice together. Find the height of the cone that maximizes the volume. (https://youtu.be/ZNoJThDRBcw)
Find the point on the parabola that is closest to the point . (https://youtu.be/ZZYf4hzluKw)
| Day | Section | Topic |
|---|---|---|
| Mon, Apr 1 | class canceled | |
| Wed, Apr 3 | 4.6 | Limits at infinity and asymptotes |
| Thu, Apr 4 | Review | |
| Fri, Apr 5 | 4.8 | L’Hospital’s rule |
We started with this optimization example which we did not get to last time.
Then we introduced limits as approaches infinity. The key idea when taking the limit of a polynomial expression as is to factor out the highest power of . We used that idea on all of these examples:
Find and when (https://youtu.be/qNhV2S2whyw)
Here are a few more examples we didn’t have time for in class.
Today we introduced L’Hospital’s rule which is a fast way to calculate limits when you have an indeterminant form or . We did these examples.
.
.
. (You can’t use L’Hospital’s rule here! Why not?)
(Hint: The key to this one is to factor out the highest power of in the numerator & denominator).
.
| Day | Section | Topic |
|---|---|---|
| Mon, Apr 8 | 4.10 | Antiderivatives |
| Wed, Apr 10 | 4.10 | Antiderivatives - con’d |
| Thu, Apr 11 | Review | |
| Fri, Apr 12 | 5.1 | Approximating area |
Today we introduced antiderivatives also known as indefinite integrals. To find the antiderivative of a function , you just need to find a function that has as its derivative. We started with this example:
We introduced these rules for integrals:
Power Rule for Integrals. .
Addition Rule. .
Constant Multiple Rule. .
Important: Notice that there is no quotient, product, or chain rule!
We applied those rules to these examples:
We also looked at antiderivatives of trig functions
Find the antiderivative of . (https://youtu.be/EpH4rN93ftc)
We finished by discussing how you can use antiderivatives to find the velocity and position of a falling object if you know its acceleration by integrating:
Find the velocity of a falling object by integrating .
Find the position by integrating .
Today we looked at more examples of antiderivatives. We started with a theorem.
Theorem. If and are both antiderivatives of a function , then there is a constant such that .
We proved this theorem by observing that the function has derivative equal to zero everywhere. Therefore there cannot be two different points such that is different than , otherwise, the MVT would imply that would be non-zero somewhere on the interval from . Therefore the function is constant.
After proving this theorem, we talked about initial value problems. This is when you are given the derivative of a function and the value of the function at one point and are able to use integration to find the exact value of the function. We did the following examples.
Solve with initial condition . (https://youtu.be/kwGukY_2qWQ)
Solve with initial condition . (https://youtu.be/gw3jd921Zzc)
Solve given that . (https://youtu.be/tXR__A_jkxE)
Find if and the graph of passes through .
Suppose that , and . (https://youtu.be/ETixs3tYAXE)
The acceleration of gravity is feet per second squared. If a rock is thrown upwards from a platform located 20 feet above the ground with initial velocity 30 feet per second, find formulas for the height and velocity of the rock as functions of time.
Today we introduced Riemann sums as a way to approximate the area under a curve. We started with the curve as an example.
The formula for finding a Riemann sum approximation (using right endpoints) is
Riemann Sum. For any continuous function on an interval , the area under is approximately where is the number of rectangles,
We also reviewed summation notation. If you aren’t familiar, here is a good explanation:
We did the following in class:
.
. (We derived the formula
Here is another example we didn’t do:
| Day | Section | Topic |
|---|---|---|
| Mon, Apr 15 | 5.2 | The definite integral |
| Wed, Apr 17 | 5.3 | Evaluating definite integrals |
| Thu, Apr 18 | Review | |
| Fri, Apr 19 | Midterm 3 |
Today we introduced the definite integral which is defined as the limit of the Riemann sum as the number of rectangles approaches infinity: A function is integrable on an interval if this limit exists.
We approximated the following definite integrals using Desmos to calculate the Riemann sum:
Because the definite integral is the area of the curve, sometimes you can find the answer without calculus if you recognize the shape:
Another important concept is that area beneath the x-axis counts as negative area. We did this example by looking at the shapes and finding the positive and negative area.
Definite integrals have these important properties:
Constant multiple rule. For any integrable function and constant ,
Addition rule. For any integrable functions and ,
Additive interval rule. For any real numbers ,
We did the following additional examples.
Suppose that and . Find . (https://youtu.be/QcHz3h81U-s?t=305)
Suppose that and , then find (https://youtu.be/TqMxlzZiKg4)
Today we talked about
The Fundamental Theorem of Calculus. If is a function with antiderivative on an interval , then
We explained why this theorem makes sense by changing the letter to a letter to emphasize that the formula above is a function of the upper bound in the integral. And we showed that the derivative of the area function is , so it makes sense that you can use the antiderivative of to get the area.
We did these examples in class using the Fundamental Theorem of Calculus to evaluate the definite integrals.
Just like with derivatives, it is important to understand the meaning of the definite integral.
If a particle has velocity , then what is its net change in position from time until time ? (https://youtu.be/Sy_7PkoTCtA)
Water flows out of a tank at a rate liters per minute. Find the amount of water flows out of the tank in the first 10 minutes? (https://youtu.be/66L46J4rxIA)
| Day | Section | Topic |
|---|---|---|
| Mon, Apr 22 | 5.4 | Integration formulas |
| Wed, Apr 24 | 5.5 | Substitution |
| Thu, Apr 25 | Review | |
| Fri, Apr 26 | 5.5 | Substitution - con’d |
| Mon, Apr 29 | Recap & review |
Today we looked at more examples of definite integrals and we also defined:
Definition. The average value of a function on an interval is
We did a few extra problems to see some of the ideas that come up working with definite integrals.
We finished by introducing an integration technique called u-substitution which lets you undo a chain rule.
Today we went into more depth about the u-substitution method. We did the following examples.
(Hint: you don’t have to use substitution for this one, but substitution will work too.)
There is a shortcut for the last two integrals since the derivative of the inside is just a constant. When the derivative of the inside is just a constant, you can use the reverse chain rule: integrate the outside function, leave the inside alone, then divide by the derivative of the inside. Be careful, that does not work if the derivative of the inside is not a constant! We applied the reverse chain rule to
We finished with a couple more complicated u-substitution examples.
We didn’t do this last one, but it is also a good u-substitution example:
Today we talked about some of the material that we haven’t seen in a while. We reviewed continuity and limits. We looked at these examples:
Find the values of where the function is discontinuous on the interval . For each discontinuity, determine if it is a hole, a jump, or a pole discontinuity.
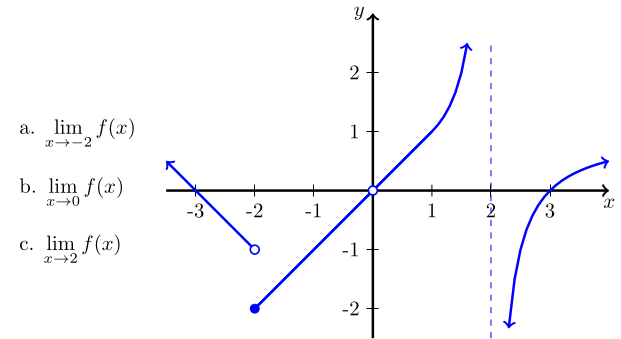
Use the graph below to find the indicated limits.