Statistics Notes

Math 121 - Fall 2024

• Class Notes
• Schedule & Syllabus
• Software & Tables

Week 1 Notes

Tentative Schedule

Mon, Aug 26

Today we covered data tables, individuals, and variables. We also talked about the difference between categorical and quantitative variables.

• Example: Class Data

1. We looked at a case of a nurse who was accused of killing patients at the hospital where she worked for 18 months. One piece of evidence against her was that 40 patients died during the shifts when she worked, but only 34 died during shifts when she wasn’t working. If this evidence came from a date table, what would be the most natural individuals (rows) & variables (columns) for that table?

• Example: Accident Fatalities by State (source: CDC)

2. In the data table in the example above, who or what are the individuals? What are the variables and which are quantitative and which are categorical?

3. If we want to compare states to see which are safer, why is it better to compare the rates instead of the total fatalities?

4. What is wrong with this student’s answer to the previous question?

Rates are better because they are more precise and easier to understand.

I like this incorrect answer because it is a perfect example of bullshit. This student doesn’t know the answer so they are trying to write something that sounds good and earns partial credit. Try to avoid writing bullshit. If you catch yourself writing B.S. on one of my quizzes or tests, then you can be sure that you a missing a really simple idea and you should see if you can figure out what it is.

Wed, Aug 28

We talked about how to summarize quantitative data. We started by reviewing the mean and median. We saw how to find the average in Excel, and we talked about how to find the position of the median in a long list of numbers (assuming they are sorted).

Then we used the class data we collected last time to introduce histograms and stem-and-leaf plots (also known as stemplots). We also talked about how to tell if data is skewed left or skewed right. One important concept is that the median is not affected by skew, but the average is pulled in the direction of the skew, so the average will be bigger than the median when the data is skewed right.

Until recently, Excel did not have an easy way to make histograms, but Google Sheets does. If you need to make a histogram, I recommend using Google Sheets or this histogram plotter tool.

• Example: US Household Income (2010)

1. Which is greater, the mean or the median household income?

2. Can you think of a distribution that is skewed left?

3. Why isn’t this bar graph from the book a histogram?

We finished with this in-class workshop.

• Workshop: Histograms & stemplots

Fri, Aug 30

We introduced the five number summary and box-and-whisker plots (boxplots). We also talked about the interquartile range (IQR) and how to use the $1.5 \times \text{IQR}$ rule to determine if data is an outlier.

• Workshop: Boxplots

Week 2 Notes

Tentative Schedule

Wed, Sep 4

Today we talked about robust statistics such as the median and IQR that are not affected by outliers and skew. We also introduced the standard deviation. We did one example of a standard deviation calculation by hand, but you won’t ever have to do that again in this class. Instead, we just use software to find standard deviation for us. We looked at how to find standard deviation in Excel using the =stdev() function.

We finished by looking at some examples of histograms that have a shape that looks roughly like a bell. This is a very common pattern in nature that is called the normal distribution.

• Example: Heights of men in the USA
• Example: Annual rainfall in Farmville, VA

The normal distribution is a mathematical model for data with a histogram that is shaped like a bell. The model has the following features:

1. It is symmetric (left & right tails are same size)
2. The mean ($\mu$) is the same as the median.
3. It has two inflection points (the two steepest points on the curve)
4. The distance from the mean to either inflection point is the standard deviation ($\sigma$).
   
5. The two numbers $\mu$ and $\sigma$ completely describe the model.

The normal distribution is a theoretical model that doesn’t have to perfectly match the data to be useful. We use Greek letters $\mu$ and $\sigma$ for the theoretical mean and standard deviation of the normal distribution to distinguish them from the sample mean $\bar{x}$ and standard deviation $s$ of our data which probably won’t follow the theoretical model perfectly.

Fri, Sep 6

We talked about z-values and the 68-95-99.7 rule.

1. The average high temperature in Anchorage, AK in January is 21 degrees Fahrenheit, with standard deviation 10. The average high temperature in Honolulu, HI in January is 80°F with σ = 8°F. In which city would it be more unusual to have a high temperature of 57°F in January?

• Workshop: Normal distributions

Week 3 Notes

Tentative Schedule

Mon, Sep 9

We reviewed some of the exercise from the workshop last Friday. Then we introduced how to find percentages on a normal distribution for locations that aren’t exactly 1, 2, or 3 standard deviations away from the mean. I strongly recommend downloading the Probability Distributions app (android version, iOS version) for your phone. We did the following examples.

1. SAT verbal scores are roughly normally distributed with mean μ = 500, and σ = 100. Estimate the percentile of a student with a 560 verbal score.

2. What percent of years will Farmville get between 40 and 50 inches of rain?

3. How much rain would Farmville get in a top 10% year?

4. Estimate the percent of men who are between 6 feet and 6’5” tall.

5. How tall are men in the 75-th percentile?

Wed, Sep 11

There was no class since I was out with COVID. Instead, there was this workshop to complete on your own.

Workshop: Normal distributions 2

Week 4 Notes

Tentative Schedule

Mon, Sep 16

We introduced scatterplots and correlation coefficients with these examples:

• Example R values.
• Height vs. Weight
• Marriage ages
• Guess the correlation

1. What would the correlation between husband and wife ages be in a country where every man married a woman exactly 10 years older? What if every man married a woman exactly half his age?

Important concept: correlation does not change if you change the units or apply a simple linear transformation to the axes. Correlation just measures the strength of the linear trend in the scatterplot.

We finished by talking about explanatory and response variables and how correlation doesn’t mean causation!

Wed, Sep 18

We talked about least squares regression. The least squares regression line has these features:

1. Slope $m = R \frac{s_y}{s_x}$
2. Point $(\bar{x}, \bar{y})$
3. y-Intercept $b = \bar{y} - m \bar{x}$

You won’t have to calculate the correlation $R$ or the standard deviations $s_y$ and $s_x$, but you might have to use them to find the formula for a regression line.

We looked at these examples:

• Blood Alcohol Content vs. Number of Beers
• Marriage ages
• Midterm exam grades

Keep in mind that regression lines have two important applications.

1. Make predictions about average y-values at different x-values.
2. The slope is the rate of change.

Fri, Sep 20

After the quiz, we talked about the coefficient of determination $R^2$ which represents the percent of the variability in the $y$-values that follow the tend, the remaining $1-R^2$ is the percent of the varibility that is above and below the trend line.

• Workshop: Lightning fatalities

Week 5 Notes

Tentative Schedule

Mon, Sep 23

We talked about the difference between samples and populations. The central problem of statistics is to use sample statistics to answer questions about population parameters.

We looked at an example of sampling from the Gettysburg address, and we talked about the central problem of statistics: How can you answer questions about the population using samples?

The reason this is hard is because sample statistics usually don’t match the true population parameter. There are two reasons why:

• Bias: systematic error (each source has error in a particular direction)
• Random error: non-systematic error

We looked at this case study:

• Gallup polling & sample bias

Important Concepts.

1. You can avoid/reduce random error by choosing a large sample.

2. Large samples don’t reduce bias.

3. The only sure way to avoid bias is a simple random sample.

Wed, Sep 25

We started with this workshop (just the front page).

• Workshop: Random error versus bias

Then we talked about the review problems for the midterm on Friday.

Week 6 Notes

Tentative Schedule

Mon, Sep 30

Recall that correlation is not causation. The only way to prove that one (explanatory) variable is the cause of a response is to use a randomized controlled experiment. We looked at these examples.

1. A study try to determine whether cellphones cause brain cancer. The researchers interviewed 469 brain cancer patients about their cellphone use between 1994 and 1998. They also interviewed 469 other hospital patients (without brain cancer) who had the same ages, genders, and races as the brain cancer patients.

   1. What was the explanatory variable?
   2. What was the response variable?
   3. Which variables were controlled?
   4. Was this an experiment or an observational study?
   5. Are there any possible lurking variables?

2. In 1954, the polio vaccine trials were one of the largest randomized controlled experiments ever conducted. Here were the results.

   1. What was the explanatory variable?
   2. What was the response variable?
   3. This was an experiment because it had a treatment variable. What was that?
   4. Which variables were controlled?
   5. Why don’t we have to worry about lurking variables?

We talked about why the polio vaccine trials were double blind and what that means.

3. Do magnetic bracelets work to help with arthritis pain?

   1. What is the explanatory variable?
   2. What is the response variable?
   3. How hard would it be to design a randomized controlled experiment to answer the question above?

We finished by talking about anecdotal evidence.

Wed, Oct 2

Today we introduced probability models which always have two parts:

1. A list of possible outcomes called a sample space.
2. A probability function $P(E)$ that gives the probability for any subset $E$ of the sample space.

A subset of the sample space is called an event. We already intuitively know lots of probability models, for example we described the following probability models:

1. Flip a coin.

2. Roll a six-sided die.

3. If you roll a six-sided die, what is $P(\text{result is even})?$

4. The proportion of people in the US with each of the four blood types is shown in the table below.

   Type	O	A	B	AB
   Proportion	0.45	0.40	0.11	?

   What is $P(\text{Type AB})?$

• Workshop: Probability distributions

Fri, Oct 4

We talked about the addition and multiplication rules for disjoint and independent events.

1. If you shuffle a deck of 52 playing cards, and then draw one card, what is $P(\text{Ace})$?
2. If you shuffle a deck of 52 playing cards, and then draw one card, what is $P(\text{Heart})$?
3. Is the event that you get an Ace and the event that you get a Heart disjoint? Are they independent?
   
4. What if you draw the top two cards from the deck. Are the events $A = \text{First card is an ace}$ and $B = \text{Second card is an ace}$ independent?

• Workshop: Basic probability rules

Week 7 Notes

Tentative Schedule

Mon, Oct 7

Today we talked about weighted averages. To find a weighted average:

1. Multiply each number by its weight.
2. Add the results.

We did an two examples.

1. Calculate the final grade of a student who gets an 80 quiz average, 72 midterm average, 95 project average, and an 89 on the final exam.

2. Eleven nursing students graduated from a nursing program. Four students completed the program in 3 years, four took 4 years, two took 5 years, and one student took 6 years to graduate. Express the average time to complete the program as a weighted average.

We also talked about expected value (also known as the theoretical average) which is the weighted average of the outcomes in a probability model, using the probabilities as the weights.

• Workshop: Expected value & weighted averages

We finished by talking about the Law of Large Numbers which says: when you repeat a random experiment many times, the sample mean tends to get closer to the theoretical average.

Wed, Oct 9

A random variable is a probability model where the outcome are numbers. We often use a capital letter like $X$ or $Y$ to represent a random variable. We use the shorthand $E(X)$ to represent the expected value of a random variable. Recall that the expected value (also known as the theoretical average) is the weighted average of the possible outcomes weighted by their probabilities.

A probability histogram shows the probability distribution of a random variable. Every probability distribution can be described in terms of the following three things:

1. Shape - is it shaped like a bell, or skewed, or something even more complicated?
2. Center - the theoretical average $\mu$ (i.e., the expected value)
3. Spread - the theoretical standard deviation $\sigma$

In the game roulette there is a wheel with 38 slots. The slots numbered 1 through 36 are split equally between black and red slots. The other two slots are 0 and 00 which are green. When you spin the wheel, you can bet that the ball will land in a specific slot or a specific color. If you bet $1, and the ball lands on the specific number you picked, then you win $36.

1. Find the expected value of your bet.

2. Draw a probability histogram for this situation.

3. Describe the shape of the distribution.

4. What does the law of large numbers predict will happen if you play many games of roulette?

We also looked at what happens if you bet $1 on a color like black. Then you win $2 if it lands on black. It turns out that the expected value is the same, but the distribution has a different shape (more skewed) and much larger spread ($\sigma = \$0.9986$ for betting on a number versus $\sigma = \$5.763$ if you bet on black).

We finished by talking about the trade-off between risk ($\sigma$) versus expected returns ($\mu$) when investing. We also looked at what happens if you play a lot of games of roulette using this app.

Fri, Oct 11

Suppose we are trying to study a large population with mean $\mu$ and standard deviation $\sigma$. If we take a random sample, the sample mean $\bar{x}$ is a random variable and its probability distribution is called the sampling distribution of $\bar{x}$. Assuming that the population is large and our sample is a simple random sample, the sampling distribution always has the following features:

Examples of sampling distributions.

• Gettysburg Address words
• Weights of adults
• NFL kickoffs

1. The average American weighs $\mu = 170$ lbs. with a standard deviation of $\sigma = 40$ lbs. If a commuter plan is designed to seat 22 passengers, what is the probability that the combined weight of the passengers would be greater than $4{,}000$ lbs?

Week 8 Notes

Tentative Schedule

Wed, Oct 16

We started with this warm-up problem which is a review of the things we talked about last week.

1. Before state lotteries, mobsters used to run illegal lotteries called the numbers game in many cities. It cost 1 dollar to buy a numbers game lottery ticket and players could pick any three digit number from 000 to 999. If their number was picked, they would win $600.
   1. What is the expected value of a numbers ticket?
      
   2. The standard deviation for a numbers ticket was $\sigma = \$18.96$. If someone played the numbers game every day (350 days per year) for 40 years, that would be 14,000 games. Describe the sampling distribution for this person’s average winnings per game. Is it possible they win more than $1 per game?
      
   3. The mobster Casper Holstein took as many as 150,000 bets per week. How likely would it be for the mob to have a bad week where they lost money?

Then we talked about sample proportions which are denoted $\hat{p}$. In a SRS from a large population, $\hat{p}$ is random with sampling distribution that has the following features.

We did the following exercises in class.

1. In our class, 13 out of 28 students were born in VA. Is $\frac{13}{28}$ a statistic or a parameter? Should you denote it as $p$ or $\hat{p}$?

2. Assuming that the true proportion of all HSC students that were born in VA is 50%, describe the sampling distribution for $\hat{p}_\text{VA}$ in a random sample of $N = 25$ students.

3. About one third of American households have a pet cat. If you randomly select $N = 50$ households, describe the sampling distribution for the proportion that have a pet cat.

4. According to a 2006 study of 80,000 households, 31.6% have a pet cat. Is 31.6% a statistic or a parameter? Would it be better to use the symbol $\hat{p}$ or $p$ to represent it?

Fri, Oct 18

Last time we saw that $\hat{p}$ is a random variable with a sampling distribution. We started today with this exercise from the book:

• Exercise 5.4

Then we talked about the following simple idea: there is a 95% chance that $\hat{p}$ is within 2 standard deviations of the true population proportion $p$. So if we want to estimate what the true $p$ is, we can use a 95% confidence interval: $$\hat{p} \pm 2 \sqrt{\frac{\hat{p}(1- \hat{p}}{N}}.$$

The confidence interval formula has two parts: a best guess estimate (or point estimate) before the plus/minus symbol, and a margin of error after the $\pm$ symbol. The formula for the margin of error is 2 times the standard error which is an approximation of $\sigma_{\hat{p}}$ using $\hat{p}$ instead of $p$.

1. In our class 13 out of 28 students were born in VA. Use the 95% confidence interval formula to estimate the percent of all HSC students that were born in VA.

Week 9 Notes

Tentative Schedule

Mon, Oct 21

Today we talked about confidence intervals for a population proportion again. We talked about how you can change the confidence level by adjusting the critical z-value $z^*$.
$$\hat{p} \pm z^* \sqrt{ \frac{\hat{p}(1-\hat{p})}{N}}.$$

Examples.

1. In 2004 the General Social Survey found 304 out 977 Americans always felt rushed. Find the margin of error for a 90% confidence interval with this data.

2. What are we 90% sure is true about the confidence interval we found? Only one of the following is the correct answer. Which is it?

   1. 90% of Americans are in the interval.
   2. 90% of future samples will have results in the interval.
   3. 90% sure that the population proportion is in the interval.
   4. 90% sure that the sample proportion is in the interval.

Confidence intervals for proportions are based on some big assumptions.

1. No Bias. The data must be a simple random sample from the population to avoid bias.

2. Normality. The sample size must be large enough for $\hat{p}$ to be normally distributed. A rule of thumb (the success-failure condition) is that you should have at least 15 “successes” and 15 “failures” in your data in order to use this kind of confidence interval.

We finished with one more exercise.

3. A 2017 Gallop survey of 1,011 American adults found that 38% believe that God created man in his present form. Find the margin of error for a 95% confidence interval to estimate the percent of all Americans who share this belief.

Wed, Oct 23

We talked about the midterm 2 review in class today. The solutions are online too.

Week 10 Notes

Tentative Schedule

Mon, Oct 28

Today we introduced hypothesis testing. This is a tool for answering yes/no questions about a population parameter. You start by considering two possible hypotheses about the parameter of interest.

• Null Hypothesis ($H_0$) - is a specific claim about the parameter.
• Alternative Hypothesis ($H_A$) - is what must be true if the null hypothesis is false.

Here are the steps to do a hypothesis test for a single proportion:

1. State the hypotheses. These will pretty much always look like

   • $H_0 ~:~ p = p_0$
   • $H_A ~:~ p \ne p_0$
     where $p_0$ is a specific proportion that makes sense in the context of the situation.

2. Calculate the test statistic. Using the formula $$z = \frac{\hat{p} - p_0}{\sqrt{\frac{p_0(1-p_0)}{N}}}.$$

3. Find the p-value. The p-value is the probability of getting a result at least as extreme as the sample statistic if the null hypothesis is true.

4. Explain what it means. A low p-value is evidence that we should reject the null hypotheses. Usually this means that the results are too surprising to be caused by random chance along. A p-value over 5% means we definitely should not reject $H_0$.

We did two full examples in class. For each example, you should be able to do each of the four steps above to test the hypotheses.

1. When I was a kid, I took a test to see if I had psychic powers. In the test, I had 25 chances to guess which one of five symbols was on 25 different cards that I couldn’t see. If I were just guessing, I would only have a 20% (1 out of 5) of guessing right. But I actually got 10 out of 25 guesses correct. How strong is this evidence that I am psychic?

2. 13 out of 28 students (46.4%) in our class were born in VA. Is this strong evidence that less than half of all HSC students were born in VA.

One other example we didn’t have time to finish was this one.

Wed, Oct 30

We reviewed the steps for doing a hypothesis test about a population proportion. The we did this example that we ran out of time for last time:

1. In 2013, a random sample of 1028 U.S. adults found that 56% support nuclear arms reduction. Does this provide strong evidence that a majority of Americans support nuclear arms reduction?

We talked about how the null hypotheses must give a specific value for the parameter of interest so that we can create a null model that we can test. If the sample statistic is far from what we expect, then we can reject the null hypothesis and say that the results are statistically significant. Unlike in English, the word significant does not mean “important” in statistics. It actually means the following.

Notice that all of the items on the list above are statistics jargon except item 5.

We finished with two exercises from the book.

2. Exercise 5.16

Notice that in 5.16(b), you could make the case that we have prior knowledge based on the reputation of the state of Wisconsin to guess that that percent of people who have drank alcohol in the last year in Wisconsin (which we denoted $p_{WI}$) satisfies a one-sided alternative hypothesis: $$H_A ~:~ p_\text{WI} > 70\%.$$ If you don’t know about Wisconsin, then you should definitely use the two-sided alternative hypothesis: $$H_A ~:~ p_\text{WI} \ne 70\%$$ The only difference is when you calculate the p-value, you use two tails of the bell curve if you are doing a two-sided p-value. If you aren’t sure, it is always safe to use a two-sided alternative.

3. Exercise 5.17

Fri, Nov 1

When we do a hypothesis test, we need to make sure that the assumptions of a hypothesis test are satisfied. There are two that we need to check:

1. No Bias. Data should come from a simple random sample (SRS) from the population.
2. Normality. Sample size should be large enough to trust that $\hat{p}$ will be normally distributed. Based on the $p_0$ from the null hypothesis, you should expect at least 10 success and 10 failures. So you need both $$n p_0 \ge 10 \text{ and } n (1-p_0) \ge 10.$$ In practice, the normality assumption is usually satisfied as long as there are at least 15 successes and 15 failures in the sample.

We looked at whether these two assumptions are satisfied for this example:

1. In our first example of a hypothesis test we looked at an example where I got 10 out of 25 guesses correct with Zenner cards. Does that example satisfy the assumptions above?

Another thing you have to decide when you do a hypothesis test is how strong the evidence needs to be in order to convince you to reject the null hypothesis. Historically people aimed for a significance level of $\alpha = 5\%$. A p-value smaller than that was usually considered strong enough evidence to reject $H_0$. Now people often want stronger evidence than that, so you might want to aim for a significance level of $\alpha = 1\%$. I’m some subjects like physics where things need to be super rigorous they use even lower values for $\alpha$. Unlike the p-value, you pick the significance level $\alpha$ before you look at the data.

If $H_0$ is true, then the significance level $\alpha$ that you choose is the probability that you will make a type I error which is when you reject $H_0$ when you shouldn’t. The disadvantage of making $\alpha$ really small is that it does increase the chance of a type II error which is when you don’t reject $H_0$ even though you should.

In a criminal trial the prosecution tries to prove that the defendant is “guilty beyond a reasonable doubt”. Think of a type I error as when the jury convicts an innocent defendant. A type II error would be if the jury does not convict someone who is actually guilty.

Week 11 Notes

Tentative Schedule

Mon, Nov 4

Today we talked about two-sample hypothesis tests for proportions. We did two examples in class:

1. In the 2008 General Social Survey, people were asked to rate their lives as exciting, routine, or dull. 300 out of 610 men in the study said their lives were exciting versus 347 out of 739. Is that strong evidence that there is a difference between the proportions of men and women who find their lives exciting?

2. In 2012, the Atheist Shoe Company noticed that packages they sent to customers in the USA were never arriving. So they did an experiment. They mailed 89 packages that were clearly labeled with the Atheist brand logo, and they also sent 89 unmarked packages in plain boxes. 9 out of the 89 labeled packages did not arrive on time compared with only 1 out of 89 unlabeled packages. Is that a statistically significant difference? (See this website for more details: Atheist shoes experiment)

In both examples we used the following theory. In a large enough random sample from two populations A and B, the gap between the sample proportions $\hat{p}_A - \hat{p}_B$ has a sampling distribution with:

• Shape: Approximately normal.
• Center: Equal to the true population gap $p_A - p_B$.
• Spread: The standard deviation is $$\sqrt{\frac{p_A(1-p_A)}{N_A} + \frac{p_B(1-p_B)}{N_B}}.$$

From this theory we talked about how to test the following hypotheses:

• $H_0 ~:~ p_A = p_B$
• $H_A ~:~ p_A \ne p_B$

using the test statistic: $$z = \frac{\hat{p}_A - \hat{p}_B}{\sqrt{\hat{p}(1- \hat{p})\left(\frac{1}{N_A} + \frac{1}{N_B}\right)}}$$ where $\hat{p}$ is the pooled proportion: $$\hat{p} = \frac{\text{ Total number of successes in both groups }}{\text{ Combined sample size }}.$$

You do need a big enough sample for the normality assumption to hold, and you need the samples to not be biased. A rule of thumb for the sample size is that you should have at least 5 successes and failures for each group.

If we want to estimate how big the gap between the population proportions $p_A$ and $p_B$ is, then you can use a two-sample confidence interval for proportions: $$(\hat{p}_A - \hat{p}_B) \pm z^* \sqrt{\frac{\hat{p}_A (1-\hat{p}_A)}{N_A} + \frac{\hat{p}_B (1- \hat{p}_B)}{N_B}}.$$

Because the formulas for two-sample confidence intervals and hypothesis tests are so convoluted, I posted an interactive formula sheet under the software tab of the website. Feel free to use it on the projects when you need to calculate these formulas.

Two sample confidence intervals for proportions are a little less robust than hypothesis tests. It is recommended that you should have at least 10 successes & 10 failures in each group before you put much trust in the interval.

Wed, Nov 6

We started with this example:

1. A study in the early 1990s looked at whether the anti-retroviral drug AZT is effective at preventing HIV-positive pregnant women from passing the HIV virus on to their children. In the study, 13 out of 180 babies whose mothers were given AZT while pregnant tested postive for HIV, compared with 40 out of 183 babies whose mothers got a placebo. Is this strong evidence that AZT is effective? How much of a difference does it make?

Then we did a workshop.

• Workshop: High school drug testing

Fri, Nov 8

We reviewed statistical inference which is the process of using sample statistics to say something about population parameters. There are two main techniques:

• Hypothesis testing - Answers a yes/no question about a parameter
• Confidence interval - Estimates the value of a parameter

We have been focused on inference about proportions of a categorical variable. Today we started talked about how to do inference about a quantitative variable like height. We looked at our class data and saw that the sample mean height is $\bar{x}_{HS} = 71.8$ inches. That suggests that maybe Hampden-Sydney students are taller than average for men in the United States. So we made these hypotheses:

• $H_0: \mu_{HS} = 70$
• $H_A: \mu_{HS} > 70$

To test these, we reviewed what we know about the sampling distribution for $\bar{x}$, and we tried to find the z-value using the formula $$z = \frac{\bar{x} - \mu_0}{\sigma / \sqrt{n}}.$$ Unfortunately, we don’t know the population standard deviation $\sigma$ for all HSC students. We only know the sample standard deviation which was $s = 2.7$ inches. If we use that instead of $\sigma$, then we get a t-value: $$t = \frac{\bar{x} - \mu_0}{s / \sqrt{n}}.$$ which follows a t-distribution. We talked about how to use the t-distribution app to calculate probabilities on a t-distribution. One weird thing about t-distributions is that they have degrees of freedom (denoted by either df or $\nu$). When you do a hypothesis test for one mean or a confidence interval for one mean, $$\text{degrees of freedom} = n - 1.$$ We briefly talked about why this is. Then we used the app to find a p-value for our class data and see whether or not we have strong evidence that HSC students are taller on average than other men in the USA. The logic of p-values is exactly the same for a t-test as it is for a hypothesis test with the normal distribution.

Week 12 Notes

Tentative Schedule

Mon, Nov 11

A t-distribution confidence interval is a tool to estimate the value of a population mean ($\mu$): $$\bar{x} \pm t^* \frac{s}{\sqrt{n}}.$$

In order to use this formula, you need to find the critical t-value $t^*$ for the confidence level you want. The easiest way is to look up the $t^*$ value on a table.

• Table: t-distribution table

We talked about how to use the table to find $t$-values. Then we did the following examples.

1. Use the class data to make a 95% confidence interval for the average height of all HSC students.

2. Use the class data to make a 90% confidence interval for the average weight of all HSC students.

We also did this workshop.

• Workshop: Quarters

t-distribution methods require the following assumptions:

1. No Bias. Data should be a simple random sample from the population.

2. Normality. The sampling distribution for $\bar{x}$ should be normal. This tends to be true if the sample size is big. Here is a quick rule of thumb:

   • Large samples If $N \ge 30$, then the normality assumption is probably reasonable as long as the data isn’t extremely skewed or has large outliers.
     
   • Small samples If $N < 30$, then even a little skew or outliers could mess up the p-values or confidence levels you get from the t-distribution formulas.

Wed, Nov 13

One interesting mistake came up in a couple of the Project 1 write-ups. The confidence interval for the difference in survival rates for the two groups of monkeys ranges from 3% lower with calorie restriction to 35% higher. Several people said that because most of the interval is positive, that means we can conclude that calorie restriction probably increases survival rates. That is actually not true! The mathematics that lets us make a confidence interval don’t tell us anything about where the true parameter falls within the interval. So we have to be very careful about using a confidence interval or hypothesis test to say more than what it actually says.

After that, we talked about comparing the averages of two correlated variables. You can use one sample t-distribution methods to do this as long as you focus on the matched pairs differences. The key is to focus on the difference or gap between the variables. For a matched pairs t-test, we always use the following:

1. Does the data in this sample of couples getting married provide significant evidence that husbands are older than their wives on average? What is the average age gap? Use a one-sample hypothesis test and confidence interval for the average difference.

2. Are the necessary assumptions for a t-test and a t-confidence interval satisfied in the previous example?

3. Do helium filled footballs go farther when you kick them? An article in the Columbus Dispatch from 1993 described the following experiment. One football was filled with helium and another identical football with regular air. Each football was kicked 39 times and the two footballs alternated with each kick. The distances traveled by the balls on each kick is recorded in this spreadsheet: Helium filled footballs.

   Does this data provide statistically significant evidence that helium filled footballs go farther when kicked?

Fri, Nov 15

Today we introduced the last two inference formulas from the interactive formula sheet: two sample inference for means. We looked at this example which is from a study where college student volunteers wore a voice recorder that let the researchers estimate how many words each student spoke per day.

• Men vs. women words per day

We made side-by-side box and whisker plots for the data:

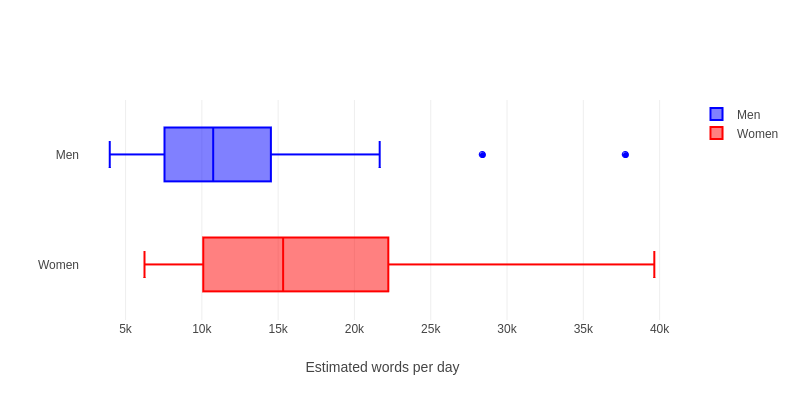
This picture suggests that there might be a difference between men & women, but is it really significant? Or could this just be a random fluke? To find out, we can do a two sample t-test.

When you do a two sample t-test (or a 2-sample t-confidence interval), there is a complicated formula for the right degrees of freedom. But an easy safe approximation is this: $$dF = \min(n_1, n_2) - 1$$ in other words, use the smaller sample size minus 1 as the degrees of freedom.

Here is a quick summary of the numbers we need to calculate the t-value for the example with men & women talking.

1. Is this statistically significant evidence that women talk more than men? Carry out all 4-steps of the hypothesis test including (i) making hypotheses, (ii) finding the t-value, (iii) finding the p-value, and (iv) explaining what it means.

Cloud Seeding. An experiment done in the 1970’s looked at whether it is possible to spray clouds with a silver iodide solution to increase the amount of rain that falls in an area. On 26 days with promising clouds a plane sprayed the clouds with silver iodide solution and on 26 similar days they didn’t spray. The amount of rainfall (measured in acre-feet) was tracked by radar. Here were the results:

2. Is there statistically significant evidence that cloud seeding works to produce more rain?

3. Use the two sample t-confidence interval to estimate how much more rain cloud seeding would produce on average.

$$(\bar{x}_1 - \bar{x}_2) \pm t^* \sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}.$$

Week 13 Notes

Tentative Schedule

Mon, Nov 18

Today we started by talking about the assumptions of the two-sample t-methods (both hypothesis tests and confidence intervals).

1. No Bias. As always, we need good simple random samples to avoid bias.

2. Normality. The t-distribution methods are based on the normal distribution. If the sample sizes are big enough, then you don’t need to worry to much about normality. Two-sample t-distribution methods are very robust, which means they tend to work well even with data that isn’t quite normal.

   • Large samples. As long as $n_1 + n_2 \ge 30$, then you are probably safe unless your data is extremely skewed or has huge outliers.
   • Small samples. If $n_1 + n_2 < 30$, then be careful relying on the results unless the data has no outliers and very little skew.

We did this example:

1. In a random sample of students who took the SATs twice found 427 had paid for coaching before their second try and 2733 had not. The table below shows the average improvements of both groups on their Verbal SAT scores:
   

   	$\bar{x}_\text{gain}$	$s$	$n$
   Coached	29	59	427
   Not	21	52	2,733

   
   A 2-sample t-test has a t-value of $t = 2.646$ which has a corresponding p-value of $0.4\%$. Explain what that means about coaching and the SATs?

2. Use a 2-sample confidence interval to estimate how much more students would gain with coaching than without.

3. How are the results of the 2-sample confidence interval different than the 1-sample confidence intervals we could construct for each group?

• Workshop: Garcinia cambogia

Wed, Nov 20

Today we reviewed for the midterm. We talked about three questions you should ask to decide which inference formula(s) to use:

We also did some of the midterm 3 review problems in class. We did this additional exercise that was not on the review:

• Exercise 7.18

We also reviewed the logic of hypothesis testing Finally, don’t forget to memorize the definition of a p-value!

Week 14 Notes

Tentative Schedule

Mon, Nov 25

Recall the difference between type I and II errors.

The best way to avoid Type II errors is to use big sample sizes. But how big is big enough? One way to tell is to estimate the margin of error based on plausible guesses about the data you might see.

We did this workshop in class:

• Workshop. Effect size & power

Week 15 Notes

Tentative Schedule

Mon, Dec 2

We started by reviewing a really important concept: association is not causation. In Project 3 we saw that there is a strong (statistically significant) association between whether states increased speed limits and the percent change in traffic fatalities. The difference was probably not a random fluke, but we can’t conclude that it was definitely the speed limit change that caused the increase in fatalities. That’s because there might be other lurking variables that we haven’t ruled out (maybe some of those states also changed their alcohol laws, or the rules about teenage drivers).

Being able to say that an association is statistically significant is useful, but it is not the same as proving cause-and-effect.

This week we are going to introduce one more inference technique known as the chi-squared test for association. The $\chi^2$ statistic let’s you measure if an association between two categorical variables is statistically significant. Before we talked about the statistic, we looked at two-way tables. We talked about how to find row and column percentages in a two-way table.