Statistics Notes

Math 121 - Fall 2025

• Class Notes
• Schedule & Syllabus
• Software & Tables

Week 1 Notes

Mon, Aug 25

Today we covered data tables, individuals, and variables. We also talked about the difference between categorical and quantitative variables.

• Example: Class Data (section 04, section 05)

1. We looked at a case of a nurse who was accused of killing patients at the hospital where she worked for 18 months. One piece of evidence against her was that 40 patients died during the shifts when she worked, but only 34 died during shifts when she wasn’t working. If this evidence came from a date table, what would be the most natural individuals (rows) & variables (columns) for that table?

• Example: Accident Fatalities by State (source: CDC)

2. In the data table in the example above, who or what are the individuals? What are the variables and which are quantitative and which are categorical?

3. If we want to compare states to see which are safer, why is it better to compare the rates instead of the total fatalities?

4. What is wrong with this student’s answer to the previous question?

Rates are better because they are more precise and easier to understand.

I like this incorrect answer because it is a perfect example of bullshit. This student doesn’t know the answer so they are trying to write something that sounds good and earns partial credit. Try to avoid writing bullshit. If you catch yourself writing B.S. on one of my quizzes or tests, then you can be sure that you a missing a really simple idea and you should see if you can figure out what it is.

Wed, Aug 27

Today we did our first in-class workshop:

• Workshop: Histograms & stemplots

Before that, we talked about how to summarize data. We talked briefly about making bar charts for categorical data. Then we used the class data we collected last time to introduce histograms and stem-and-leaf plots (also known as stemplots).

We talked about how to tell if data is skewed left or skewed right. We also reviewed the mean and the median.

We finished by talking about these examples.

• Example: US Household Income (2023)

1. Which is greater, the mean or the median household income?

2. Can you think of a distribution that is skewed left?

3. Why isn’t this bar graph from the book a histogram?

Until recently, Excel did not have an easy way to make histograms, but Google Sheets does. If you need to make a histogram, I recommend using Google Sheets or this histogram plotter tool.

Fri, Aug 29

We introduced the five number summary and box-and-whisker plots (boxplots). We also talked about the interquartile range (IQR) and how to use the $1.5 \times \text{IQR}$ rule to determine if data is an outlier.

• Workshop: Boxplots

We started with this simple example:

1. An 8 man crew team actually includes 9 men, the 8 rowers and one coxswain. Suppose the weights (in pounds) of the 9 men on a team are as follows:

    120  180  185  200  210  210  215  215  215

   Find the 5-number summary and draw a box-and-whisker plot for this data. Is the coxswain who weighs 120 lbs. an outlier?

Week 2 Notes

Wed, Sep 3

Today we talked about robust statistics such as the median and IQR that are not affected by outliers and skew. We also introduced the standard deviation. We did this one example of a standard deviation calculation by hand, but you won’t ever have to do that again in this class.

1. 11 students just completed a nursing program. Here is the number of years it took each student to complete the program. Find the standard deviation of these numbers.

    3  3  3  3  4  4  4  4  5  5  6

From now on we will just use software to find standard deviation. In a spreadsheet (Excel or Google Sheets) you can use the =STDEV() function.

2. Which of the following data sets has the largest standard deviation?

   1. 1000, 998, 1005
   2. 8, 10, 15, 20, 22, 27
   3. 30, 60, 90

We finished by looking at some examples of histograms that have a shape that looks roughly like a bell. This is a very common pattern in nature that is called the normal distribution.

• Example: Heights of men in the USA
• Example: Annual rainfall in Farmville, VA

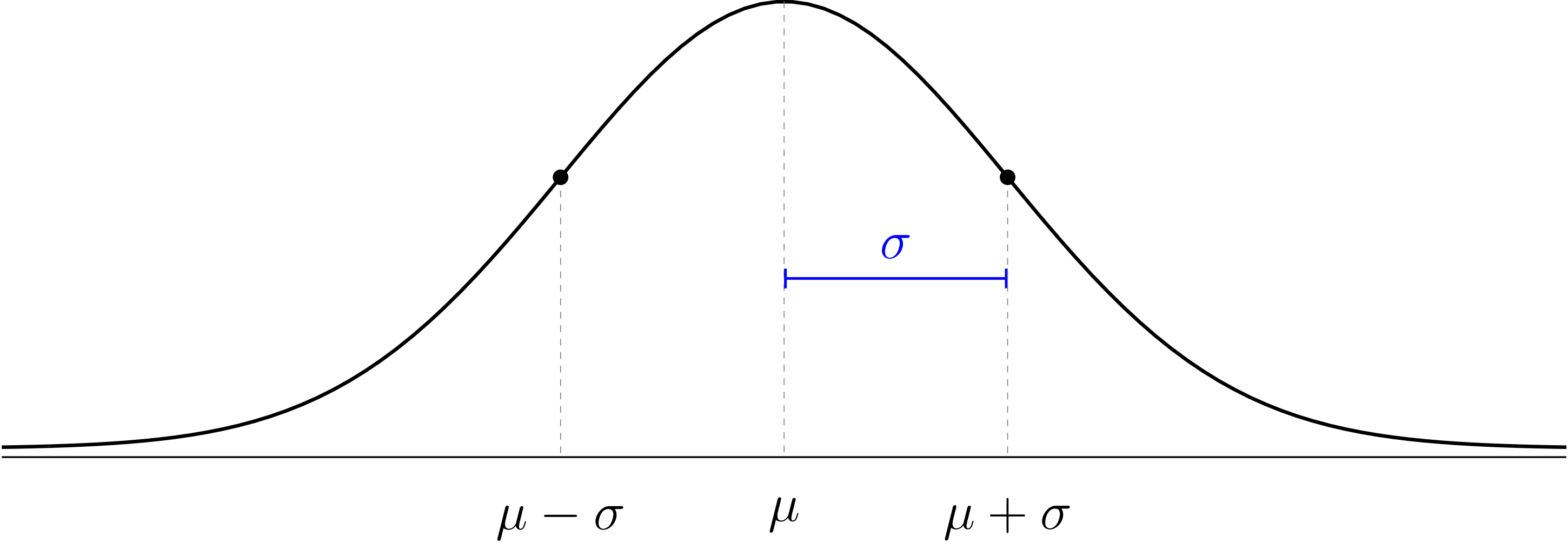
The normal distribution is a mathematical model for data with a histogram that is shaped like a bell. The model has the following features:

1. It is symmetric (left & right tails are same size)
2. The mean ($\mu$) is the same as the median.
3. It has two inflection points (the two steepest points on the curve)
4. The distance from the mean to either inflection point is the standard deviation ($\sigma$).
   
5. The two numbers $\mu$ and $\sigma$ completely describe the model.

The normal distribution is a theoretical model that doesn’t have to perfectly match the data to be useful. We use Greek letters $\mu$ and $\sigma$ for the theoretical mean and standard deviation of the normal distribution to distinguish them from the sample mean $\bar{x}$ and standard deviation $s$ of our data which probably won’t follow the theoretical model perfectly.

Fri, Sep 5

We talked about z-values and the 68-95-99.7 rule.

• Workshop: Normal distributions

We also did these exercises before the workshop.

1. In 2020, Farmville got 61 inches of rain total (making 2020 the second wettest year on record). How many standard deviations is this above average?

2. The average high temperature in Anchorage, AK in January is 21 degrees Fahrenheit, with standard deviation 10. The average high temperature in Honolulu, HI in January is 80°F with σ = 8°F. In which city would it be more unusual to have a high temperature of 57°F in January?

Week 3 Notes

Mon, Sep 8

We introduced how to find percentages on a normal distribution for locations that aren’t exactly 1, 2, or 3 standard deviations away from the mean. I strongly recommend downloading the Probability Distributions app (android version, iOS version) for your phone. We did the following examples.

1. Finding the percentile from a location on a bell curve. SAT verbal scores are roughly normally distributed with mean μ = 500, and σ = 100. Estimate the percentile of a student with a 560 verbal score.

2. Finding the percent between two locations. What percent of years will Farmville get between 40 and 50 inches of rain?

3. Converting a percentile to a location. How much rain would Farmville get in year that was in the 90th percentile?

We also talked about the shorthand notation $$P(40 < X < 50)$$ while literally means “the probability that the outcome X is between 40 and 50”.

4. What is the percentile of a man who is 6 feet tall (72 inches)?

5. Estimate the percent of men who are between 6 feet and 6’5” tall.

6. How tall are men in the 80-th percentile?

7. Men have an foot print length that is approximately $N(25 \text{cm}, 4 \text{cm})$. Women’s footprints are approximately $N(19, 3)$. Find

   1. $P(\text{Man} > 22 \text{cm})$
   2. $P(\text{Woman} > 22 \text{cm})$

Wed, Sep 10

We continued practicing calculations with the normal distribution.

Workshop: Normal distributions 2

After we finished that, we talked about explanatory & response variables (see section 1.2.4 in the book).

• An article in the journal Pediatrics found an association between the amount of acetaminophen (Tylenol) taken by pregnant mothers and ADHD symptoms in their children later in life. What are the variables? Which is explanatory and which is response?

• Does your favorite team have a home field advantage? If you wanted to answer this question, you could track the following two variables for each game your team plays: Did your team win or lose, and was it a home game or away. Which of these variables is explanatory and which is response?

Fri, Sep 12

We introduced scatterplots and correlation coefficients with these examples:

• Blood Alcohol Content vs. Number of Beers
• Marriage ages
• Example R values
• Guess the correlation

1. What would the correlation between husband and wife ages be in a country where every man married a woman exactly 10 years older? What if every man married a woman exactly half his age?

Important concept: correlation does not change if you change the units or apply a simple linear transformation to the axes. Correlation just measures the strength of the linear trend in the scatterplot.

Another thing to know about the correlation coefficient is that it only measures the strength of a linear trend. The correlation coefficient is not as useful when a scatterplot has a clearly visible nonlinear trend.

Week 4 Notes

Mon, Sep 15

We talked about least squares regression. The least squares regression line has these features:

1. Slope $m = R \frac{s_y}{s_x}$
2. Point $(\bar{x}, \bar{y})$
3. y-Intercept $b = \bar{y} - m \bar{x}$

You won’t have to calculate the correlation $R$ or the standard deviations $s_y$ and $s_x$, but you might have to use them to find the formula for a regression line.

We looked at these examples:

• Blood Alcohol Content vs. Number of Beers
• Marriage ages
• Midterm exam grades

Keep in mind that regression lines have two important applications.

• Make predictions about average y-values at different x-values.
• The slope is the rate of change.

It is important to be able to describe the units of the slope.

1. What are the units of the slope of the regression line for predicting BAC from the number of beers someone drinks?

2. What are the units of the slope for predicting someone’s weight from their height?

We also introduced the following concepts.

Wed, Sep 17

• Workshop: Lightning fatalities

Before the workshop, we started with these two exercises:

1. Suppose that the correlation between the heights of fathers and adult sons is $R = 0.5$. Given that both fathers and sons have normally distributed heights with mean $70$ inches and standard deviation 3 inches, find an equation for the least squares regression line.

2. A sample of 20 college students looked at the relationship between foot print length (cm) and height (in). The sample had the following statistics: $$\bar{x} = 28.5 \text{ cm}, ~\bar{y} = 67.75 \text{ in}, ~ s_x = 3.45 \text{ cm}, ~ s_y = 5.0 \text{ in}, ~ R = 0.71$$

   1. Find the slope of the regression line to predict height ($y$) based on footprint length ($x$). Include the units and briefly explain what it means.
      
   2. If a footprint was 30 cm long, how tall would you predict the subject was?

Fri, Sep 19

We talked about the difference between samples and populations. The central problem of statistics is to use sample statistics to answer questions about population parameters.

We looked at an example of sampling from the Gettysburg address, and we talked about the central problem of statistics: How can you answer questions about the population using samples?

The reason this is hard is because sample statistics usually don’t match the true population parameter. There are two reasons why:

• Bias: systematic error (each source has error in a particular direction)
• Random error: non-systematic error

We looked at this case study:

• Gallup polling & sample bias

Week 5 Notes

Mon, Sep 22

We did this workshop.

• Workshop: Random error versus bias

Wed, Sep 24

We talked about the midterm 1 review problems.

Week 6 Notes

Mon, Sep 29

One of the hardest problems in statistics is to prove causation. Here is a diagram that illustrates the problem.

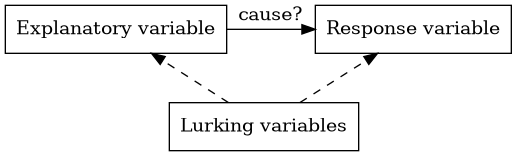
The explanatory variable might be the cause of a change in the response variable. But we have to watch out for other variables that aren’t part of the study called lurking variables.

A lurking variable that might be associated with both the explanatory and response variable is called a confounding variable.

We say that correlation is not causation because you can’t assume that there is a cause and effect relationship between two variables just because they are strongly associated. The association might be caused by lurking variables or the causal relationship might go in the opposite direction of what you expect.

We looked at these examples.

1. A study tried determine whether cellphones cause brain cancer. The researchers interviewed 469 brain cancer patients about their cellphone use between 1994 and 1998. They also interviewed 469 other hospital patients (without brain cancer) who had the same ages, genders, and races as the brain cancer patients.

   1. What was the explanatory variable?
   2. What was the response variable?
   3. Which variables were controlled?
   4. Was this an experiment or an observational study?
   5. Are there any possible lurking variables?

2. In 1954, the polio vaccine trials were one of the largest randomized controlled experiments ever conducted. Here were the results.

   1. What was the explanatory variable?
   2. What was the response variable?
   3. This was an experiment because it had a treatment variable. What was that?
   4. Which variables were controlled?
   5. Why don’t we have to worry about lurking variables?

We talked about why the polio vaccine trials were double blind and what that means.

Here is one more example we didn’t have time for:

3. Do magnetic bracelets work to help with arthritis pain?

   1. What is the explanatory variable?
   2. What is the response variable?
   3. How hard would it be to design a randomized controlled experiment to answer the question above?

We finished by talking about anecdotal evidence.

Wed, Oct 1

Today we introduced probability models which always have two parts:

1. A list of possible outcomes called a sample space.
2. A probability function $P(E)$ that gives the probability for any subset $E$ of the sample space.

A subset of the sample space is called an event. We already intuitively know lots of probability models, for example we described the following probability models:

1. Flip a coin.

2. Roll a six-sided die.

3. If you roll a six-sided die, what is $P(\text{result at least 5})?$

4. The proportion of people in the US with each of the four blood types is shown in the table below.

   Type	O	A	B	AB
   Proportion	0.45	0.40	0.11	?

   What is $P(\text{Type AB})?$

• Workshop: Probability models

Fri, Oct 3

Today we talked about the multiplication and addition rules for probability. We also talked about independent events and conditional probability. We started with these examples.

1. If you roll two six-sided dice, the results are independent. What is the probability that both dice land on a six?

2. Suppose you shuffle a deck of 52 playing cards and then draw two cards from the top. Find

   1. $P(\text{First card is an ace})$
   2. $P(\text{Second card is an ace } | \text{ first is an ace})$
   3. $P(\text{Second card is an ace } | \text{ first is not an ace})$

Then we did this workshop:

• Workshop: Basic probability rules

Week 7 Notes

Mon, Oct 6

Today we talked about weighted averages. To find a weighted average:

1. Multiply each number by its weight.
2. Add the results.

We did this workshop.

• Workshop: Expected value & weighted averages

Before that, we did some examples.

1. Calculate the final grade of a student who gets an 80 quiz average, 72 midterm average, 95 project average, and an 89 on the final exam.

2. Eleven nursing students graduated from a nursing program. Four students completed the program in 3 years, four took 4 years, two took 5 years, and one student took 6 years to graduate. Express the average time to complete the program as a weighted average.

The expected value (also known as the theoretical average) is the weighted average of the outcomes in a probability model, using the probabilities as the weights.

3. In roulette there is a wheel with 38 slots. There are 18 red slot, 18 black slots and 2 green slots. When you spin the wheel, you can bet that the ball will land on a black slot. If you bet $1, and the ball lands on black, then you win $2, otherwise you win nothing. What is the expected value for this bet?

Wed, Oct 8

Today we talked about probability distributions. A probability distribution is a probability model where the outcomes are numbers. We often use capital letters like $X$ and $Y$ as random variables. A random variable represents the possible outcome of a random experiment that follows a probability distribution. A random variable has:

• A theoretical average $E(X) = \mu_X$.
• A theoretical standard deviation $\operatorname{SD}(X) = \sigma_X$.

1. Find $E(Y)$ where $Y = \text{result of rolling a 6-sided die}$.

Every probability distribution can be described by three things:

• Shape - is it shaped like a bell, or skewed, or something even more complicated?
• Center - the theoretical average $\mu$ (i.e., the expected value)
• Spread - the theoretical standard deviation $\sigma$

2. If you play roulette and bet on one number (like 7), you have a $\tfrac{1}{38}$ chance of winning and you win $36 for every one dollar you bet.
   1. Find the expected value for a $1 bet.
   2. Draw the probability histogram. Describe the shape of the distribution.

It turns out that betting on 7 has the same expected value as betting on black, but the standard deviations are not the same ($\sigma = \$0.9986$ for betting on a number versus $\sigma = \$5.763$ if you bet on black).

We talked about the difference between continuous distributions where there is an infinite range of outcomes between any two possibilities, and discrete distributions which only have finitely many outcomes between any two possibilities. The normal distribution is continuous, rolling a six-sided die is discrete.

An important discrete probability distribution is the binomial distribution $\operatorname{Bin}(N,p)$ which counts the total number of successes when you flip a fair or unfair coin $N$ times. The number $p$ is the probability of a success on each flip.

3. Suppose you play 100 games of roulette and bet on 7 every time. Use the binomial distribution app to find the probability that you win more money than you lose.

4. What about playing 100 games and betting on black every time? Which is a better strategy?

We finished by talking about the trade-off between risk ($\sigma$) versus expected returns ($\mu$) when investing.

Fri, Oct 10

Suppose we are trying to study a large population with mean $\mu$ and standard deviation $\sigma$. If we take a random sample, the sample mean $\bar{x}$ is a random variable and its probability distribution is called the sampling distribution of $\bar{x}$. Assuming that the population is large and our sample is a simple random sample, the sampling distribution always has the following features:

Examples of sampling distributions.

• Gettysburg Address words
• Weights of adults
• NFL kickoffs

1. Every week in the Fall there are about 15 NFL games. In each game, there are about 13 kickoffs, on average. So we can estimate that there might be about 200 kickoffs in one week of NFL games. Those 200 kickoffs would be a reasonably random sample of all NFL kickoffs. Describe the sampling distribution of the average kickoff distance.

2. The average American weighs $\mu = 170$ lbs. with a standard deviation of $\sigma = 40$ lbs. If a commuter plan is designed to seat 22 passengers, what is the probability that the combined weight of the passengers would be greater than $4{,}000$ lbs? Hint: This is the same as finding $P(\bar{x} > 181.8)$

Week 8 Notes

Wed, Oct 15

We started with this warm-up problem which is a review of the things we talked about last week.

1. Annual rainfall totals in Farmville are approximately normal with mean 44 inches and standard deviation 7 inches.

   1. How likely is a year with more than 50 inches of rain?

   2. How likely is a whole decade with average annual rainfall over 50 inches?

Then we talked about sample proportions which are denoted $\hat{p}$ and can be found using the formula $$\hat{p} = \frac{\text{ number of "successes" }}{\text{ sample size }}.$$ In a SRS from a large population, $\hat{p}$ is random with a sampling distribution that has the following features.

We did the following exercises in class.

1. In my morning class, 18 out of 28 students were born in VA. Is $\frac{18}{28}$ a statistic or a parameter? Should you denote it as $p$ or $\hat{p}$? (In my afternoon class, the proportion was 10 out of 19.)

2. In the United States about 7.2% of people have type O-negative blood, so they are universal donors. Is 7.2% a parameter ($p$) or a statistic ($\hat{p}$)?

3. If a hospital has $N = 900$ patients, describe the sampling distribution for the proportion of patients who are universal donors.

4. Find the probability that $P(\hat{p}_{\text{universal donor}} > 8\%)$.

5. Assuming that the true proportion of all HSC students that were born in VA is 50%, describe the sampling distribution for $\hat{p}_\text{VA}$ in a random sample of $N = 25$ students.

6. About one third of American households have a pet cat. If you randomly select $N = 50$ households, describe the sampling distribution for the proportion that have a pet cat.

7. According to a 2006 study of 80,000 households, 31.6% have a pet cat. Is 31.6% a statistic or a parameter? Would it be better to use the symbol $\hat{p}$ or $p$ to represent it?

Fri, Oct 17

Last time we saw that $\hat{p}$ is a random variable with a sampling distribution. We started today with this exercise from the book:

• Exercise 5.4

Then we talked about the following simple idea: there is a 95% chance that $\hat{p}$ is within 2 standard deviations of the true population proportion $p$. So if we want to estimate what the true $p$ is, we can use a 95% confidence interval: $$\hat{p} \pm 2 \sqrt{\frac{\hat{p}(1- \hat{p}}{N}}.$$

The confidence interval formula has two parts: a best guess estimate (or point estimate) before the plus/minus symbol, and a margin of error after the $\pm$ symbol. The formula for the margin of error is 2 times the standard error which is an approximation of $\sigma_{\hat{p}}$ using $\hat{p}$ instead of $p$.

1. In our class 13 out of 24 students were born in VA. Use the 95% confidence interval formula to estimate the percent of all HSC students that were born in VA.

2. A 2017 Gallop survey of 1,011 American adults found that 38% believe that God created man in his present form. Find the margin of error for a 95% confidence interval to estimate the percent of all Americans who share this belief.

Week 9 Notes

Mon, Oct 20

Last time we only looked at 95% confidence intervals, but you can adjust the confidence level by using the following formula.

The variable $z^*$ is called the critical z-value is determined by the desired confidence level. Here are some common choices.

This formula works well as long as two assumptions are true:

1. No Bias. The data should come from a simple random sample to avoid bias.

2. Normality. The sample size must be large enough for $\hat{p}$ to be normally distributed. A rule of thumb (the success-failure condition) is that you should have at least 15 “successes” and 15 “failures” in the sample.

Examples.

1. In 2004 the General Social Survey found 304 out 977 Americans always felt rushed. Find the margin of error for a 90% confidence interval with this data.

2. What are we 90% sure is true about the confidence interval we found? Only one of the following is the correct answer. Which is it?

   1. 90% of Americans are in the interval.
   2. 90% of future samples will have results in the interval.
   3. 90% sure that the population proportion is in the interval.
   4. 90% sure that the sample proportion is in the interval.

3. About half of HSC students were born in Virginia. Given this fact, approximately how large of a sample of HSC students would you need to get a margin of error for a 95% confidence interval under 10%?
   

4. Case Study 5.2.4

Wed, Oct 22

We talked about the midterm 2 review in class today. The solutions are online now too.

We also did the following extra problem about conditional probability.

1. Suppose that half of the voters in one county are women. There are two candidates running, a Democrat and a Republican. 60% of the women support the Democrat, but only 35% of the men in the county do. Assume that every voter supports one of the two candidates. Find the following probabilities.

   1. P(Support Republican | Voter is male)
   2. P(Support Republican | Voter is female)
   3. P(Support Republican and voter is male)
   4. P(Support Republican and voter is female)
   5. P(Support Republican)

Week 10 Notes

Mon, Oct 27

Today we introduced hypothesis testing. This is a tool for answering yes/no questions about a population parameter. We started with this example:

1. Once I took a test to see if I had psychic powers. In the test, I had 25 chances to guess which one of five symbols was on 25 different Zenner cards (see below) that I couldn’t see. If I were just guessing, I would only have a 20% chance (1 out of 5) of guessing right. But I actually got 10 out of 25 guesses correct. How strong is this evidence that I am psychic?

Every hypothesis test starts with two possibilities:

• Null Hypothesis ($H_0$) - is a specific claim about the parameter.
• Alternative Hypothesis ($H_A$) - is what must be true if the null hypothesis is false.

Here are the steps to do a hypothesis test for a single proportion:

1. State the hypotheses. These will pretty much always look like

   • $H_0 ~:~ p = p_0$
   • $H_A ~:~ p \ne p_0$
     where $p_0$ is a specific number that makes sense in the context of the situation.

2. Calculate the test statistic. Using the formula $$z = \frac{\hat{p} - p_0}{\sqrt{\frac{p_0(1-p_0)}{N}}}.$$

3. Find the p-value. The p-value is the probability of getting a result at least as extreme as the sample statistic if the null hypothesis is true.

4. Explain what it means. A low p-value is evidence that we should reject the null hypotheses. Usually this means that the results are too surprising to be caused by random chance along. A p-value over 5% means the results might be a random fluke and we should not reject $H_0$.

2. This year 59.6% (28 out of 47) of the students in my two sections of statistics were born in VA. Is this strong evidence that more than half of all HSC students were born in VA? State the hypotheses, find the z-value, find the p-value, and explain what it means.

Wed, Oct 29

On Monday we introduced hypothesis testing:

When we do a hypothesis test, we need to make sure that the assumptions of a hypothesis test are satisfied. There are two that we need to check:

1. No Bias. Data should come from a simple random sample (SRS) from the population.
2. Normality. Sample size should be large enough to trust that $\hat{p}$ will be normally distributed. Based on the $p_0$ from the null hypothesis, you should expect at least 10 success and 10 failures. So you need both $$n p_0 \ge 10 \text{ and } n (1-p_0) \ge 10.$$

We started with this example:

1. In 2013, a random sample of 1028 U.S. adults found that 56% support nuclear arms reduction. Does this provide strong evidence that a majority of Americans support nuclear arms reduction?

We talked about how the null hypotheses must give a specific value for the parameter of interest so that we can create a null model that we can test. If the sample statistic is far from what we expect, then we can reject the null hypothesis and say that the results are statistically significant. Unlike in English, the word significant does not mean “important” in statistics. It actually means the following.

Watch out: When the evidence is weak, we don’t accept the null hypothesis. We just say the results are inconclusive and we fail to reject the null hypothesis.

We finished with these exercises from the book.

2. Exercise 5.16(b)

Notice that in 5.16(b), you could make the case that we have prior knowledge based on the reputation of the state of Wisconsin to guess that that percent of people who have drank alcohol in the last year in Wisconsin (which we denoted $p_\text{WI}$) satisfies a one-sided alternative hypothesis: $$H_A ~:~ p_\text{WI} > 70\%.$$ If you don’t know about Wisconsin, then you should definitely use the two-sided alternative hypothesis: $$H_A ~:~ p_\text{WI} \ne 70\%$$ The only difference is when you calculate the p-value, you use two tails of the bell curve if you are doing a two-sided p-value. If you aren’t sure, it is always safe to use a two-sided alternative.

3. Exercise 5.17

Fri, Oct 31

One thing you have to decide when you do a hypothesis test is how strong the evidence needs to be in order to convince you to reject the null hypothesis. Historically people aimed for a significance level of $\alpha = 5\%$. A p-value smaller than that was usually considered strong enough evidence to reject $H_0$. Now people often want stronger evidence than that, so you might want to aim for a significance level of $\alpha = 1\%$. In some subjects like physics where things need to be super rigorous they use even lower values for $\alpha$. Unlike the p-value, you pick the significance level $\alpha$ before you look at the data.

If $H_0$ is true, then the significance level $\alpha$ that you choose is the probability that you will make a type I error which is when you reject $H_0$ when you shouldn’t. The disadvantage of making $\alpha$ really small is that it does increase the chance of a type II error which is when you don’t reject $H_0$ even though you should.

In a criminal trial the prosecution tries to prove that the defendant is “guilty beyond a reasonable doubt”. Think of a type I error as when the jury convicts an innocent defendant. A type II error would be if the jury does not convict someone who is actually guilty.

After that, we introduced:

We rushed a bit at the end to squeeze in this example.

1. In the 2008 General Social Survey, people were asked to rate their lives as exciting, routine, or dull. 300 out of 610 men in the study said their lives were exciting versus 347 out of 739. Is that strong evidence that there is a difference between the proportions of men and women who find their lives exciting?

Week 11 Notes

Mon, Nov 3

We started by reviewing what we introduced last time.

As with any statistical inference method, this technique is based on two key assumptions:

• No Bias: Data should come from a simple random sample.
• Normality: Should have at least 5 successes and failures for each group.

We used the 2-sample hypothesis test on this example.

1. In 2012, the Atheist Shoe Company noticed that packages they sent to customers in the USA were getting lost in the mail. So they did an experiment. They mailed 89 packages that were clearly labeled with the Atheist brand logo, and they also sent 89 unmarked packages in plain boxes. 9 out of the 89 labeled packages did not arrive on time compared with only 1 out of 89 unlabeled packages. Is that a statistically significant difference? (See this website for more details: Atheist shoes experiment)

If you want to estimate how big the gap between the population proportions $p_A$ and $p_B$ is, then use:

Because the formulas for two-sample confidence intervals and hypothesis tests are so convoluted, I posted an interactive formula sheet under the software tab of the website. Feel free to use it on the projects when you need to calculate these formulas.

Two sample confidence intervals for proportions are a little less robust than hypothesis tests. It is recommended that you should have at least 10 successes & 10 failures in each group before you put much trust in the interval.

We started with this example:

1. A study in the early 1990s looked at whether the anti-retroviral drug AZT is effective at preventing HIV-positive pregnant women from passing the HIV virus on to their children. In the study, 13 out of 180 babies whose mothers were given AZT while pregnant tested postive for HIV, compared with 40 out of 183 babies whose mothers got a placebo. Is this strong evidence that AZT is effective? How much of a difference does it make?

Wed, Nov 5

• Workshop: High school drug testing

Fri, Nov 7

We have been focused on inference about proportions of a categorical variable. Today we started talked about how to do inference about a quantitative variable like height. This semester, my two sections of statistics have an average height of 70.94 inches with a standard deviation of 2.90 inches. This is data from 47 students. This suggests that maybe Hampden-Sydney students are taller than average for men in the United States. So we made these hypotheses:

• $H_0: \mu_{HS} = 70$
• $H_A: \mu_{HS} \ne 70$

To test these, we reviewed what we know about the sampling distribution for $\bar{x}$, and we tried to find the z-value using the formula $$z = \frac{\bar{x} - \mu_0}{\sigma / \sqrt{n}}.$$ Unfortunately, we don’t know the population standard deviation $\sigma$ for all HSC students. We only know the sample standard deviation. If we use that instead of $\sigma$, then we get a t-value: $$t = \frac{\bar{x} - \mu_0}{s / \sqrt{n}}.$$ which follows a t-distribution. We talked about how to use the t-distribution app to calculate probabilities on a t-distribution. One weird thing about t-distributions is that they have degrees of freedom (denoted by either df or $\nu$).

We briefly talked about why this is. Then we used the app to find a p-value for our class data and see whether or not we have strong evidence that HSC students are taller on average than other men in the USA. The logic of p-values is exactly the same for a t-test as it is for a hypothesis test with the normal distribution.

We finished with this example:

1. In 2017, the median home price in the USA was 254,900. Is there strong evidence that the average home price in Farmville, VA is lower than this number? Here is data from a random sample of 10 homes that sold in Farmville in 2017: $$N = 10, ~~~~~ s = 76{,}550, ~~~~~ \bar{x} = 161{,}900.$$ Carry out a hypothesis test with this data to answer the question.

Week 12 Notes

Mon, Nov 10

In order to use this formula, you need to find the critical t-value $t^*$ for the confidence level you want. The easiest way is to look up the $t^*$ value on a table. Use $n - 1$ degrees of freedom.

• Table: t-distribution table

We talked about how to use the table to find $t$-values. Then we did the following example.

1. Use the class data (section 04, section 05) to make a 95% confidence interval for the average height of all HSC students.

Here is another example that we didn’t have time for.

2. Use the class data (section 04, section 05) to make a 90% confidence interval for the average weight of all HSC students.

We also did this workshop.

• Workshop: Quarters

t-distribution methods require the following assumptions:

1. No Bias. Data should be a simple random sample from the population.

2. Normality. The sampling distribution for $\bar{x}$ should be normal. This tends to be true if the sample size is big. Here is a quick rule of thumb:

   • Large samples If $N \ge 30$, then the normality assumption is probably reasonable as long as the data isn’t extremely skewed or has large outliers.
     
   • Small samples If $N < 30$, then even a little skew or outliers could mess up the p-values or confidence levels you get from the t-distribution formulas.

Wed, Nov 12

We talked about comparing the averages of two correlated variables. You can use one sample t-distribution methods to do this as long as you focus on the matched pairs differences. The key is to focus on the difference or gap between the variables. For a matched pairs t-test, we always use the following:

1. Does the data in this sample of couples getting married provide significant evidence that husbands are older than their wives on average? What is the average age gap? Use a one-sample hypothesis test and confidence interval for the average difference.

2. Are the necessary assumptions for a t-test and a t-confidence interval satisfied in the previous example?

3. Do helium filled footballs go farther when you kick them? An article in the Columbus Dispatch from 1993 described the following experiment. One football was filled with helium and another identical football with regular air. Each football was kicked 39 times and the two footballs alternated with each kick. The distances traveled by the balls on each kick is recorded in this spreadsheet: Helium filled footballs.

   Does this data provide statistically significant evidence that helium filled footballs go farther when kicked?

Fri, Nov 14

Today we introduced the last two inference formulas from the interactive formula sheet: two sample inference for means. We looked at this example which is from a study where college student volunteers wore a voice recorder that let the researchers estimate how many words each student spoke per day.

• Men vs. women words per day

Here are side-by-side box and whisker plots for the data:

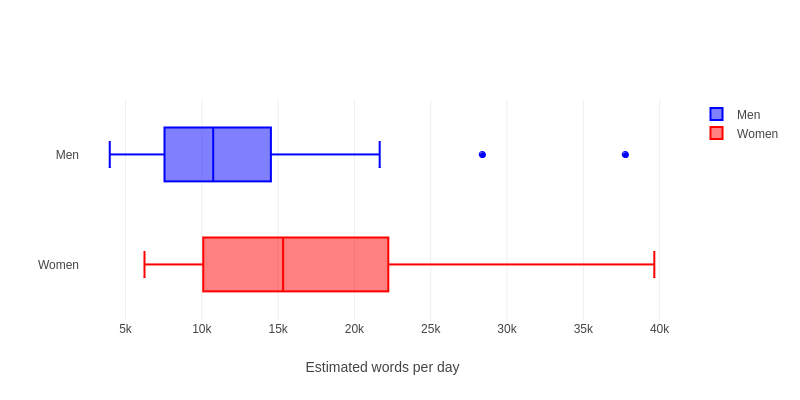
This picture suggests that there might be a difference between men & women, but is it really significant? Or could this just be a random fluke? To find out, we can do a two sample t-test.

When you do a two sample t-test (or a 2-sample t-confidence interval), there is a complicated formula for the right degrees of freedom. But an easy safe approximation is this: $$dF = \min(n_1, n_2) - 1$$ in other words, use the smaller sample size minus 1 as the degrees of freedom.

Here is a quick summary of the numbers we need to calculate the t-value for the example with men & women talking.

1. Is this statistically significant evidence that women talk more than men? Carry out all 4-steps of the hypothesis test including (i) making hypotheses, (ii) finding the t-value, (iii) finding the p-value, and (iv) explaining what it means.

Cloud Seeding. An experiment done in the 1970’s looked at whether it is possible to spray clouds with a silver iodide solution to increase the amount of rain that falls in an area. On 26 days with promising clouds a plane sprayed the clouds with silver iodide solution and on 26 similar days they didn’t spray. The amount of rainfall (measured in acre-feet) was tracked by radar. Here were the results:

2. Is there statistically significant evidence that cloud seeding works to produce more rain?

Week 13 Notes

Mon, Nov 17

Today we introduced the 2-sample confidence interval for means.

These formulas (both the two-sample t-test and t-confidence interval) are based on the same key assumptions.

• No Bias. As always, we need good simple random samples to avoid bias.

• Normality. The t-distribution methods are based on the normal distribution. If the sample sizes are big enough, then you don’t need to worry to much about normality. Two-sample t-distribution methods are very robust, which means they tend to work well even with data that isn’t quite normal.

  • Large samples. As long as $n_1 + n_2 \ge 30$, then you are probably safe unless your data is extremely skewed or has huge outliers.
  • Small samples. If $n_1 + n_2 < 30$, then be careful relying on the results unless the data has no outliers and very little skew.

1. Last time we looked at evidence that cloud seeding causes more rain to fall. Use a two sample t-confidence interval to estimate how much more rain cloud seeding would produce on average.

After that, we did this workshop in class.

• Workshop: Garcinia cambogia

Wed, Nov 19

Today we talked about the midterm 3 review problems. We also talked about how to choose the right inference method. Ask these three questions to decide which interference formula to use:

• Do you have one or two samples?
• Are you trying to estimate how big a parameter is (confidence interval) or answer a yes/no question about whether the results are significant (hypothesis test)?
  
• Are you interested in averages of a quantitative variable (means) or percentages of a categorical variable (proportions)?

The answer to these three questions will guide you to the right formula to use. We applied these questions to the following examples in class:

We also reviewed how to find p-values using the app and how to use the t-distribution table (including how to find critical z-values in addition to t-values).

One question that will definitely be on the midterm is this: what is the exact definition of a p-value? To answer this question you need to memorize:

Mon, Nov 24

Today we talked about statistical power.

We did this workshop in class:

• Workshop. Effect size & power

Week 14 Notes

Mon, Dec 1

This week we are going to introduce one more inference technique known as the chi-squared test for association. The $\chi^2$ statistic let’s you measure if an association between two categorical variables is statistically significant. Before we talked about the statistic, we looked at two-way tables. We talked about how to find row and column percentages in a two-way table.

The 2003-04 National Health & Nutrition Exam Survey asked participants how they felt about their weight (options were “underweight”, “about right”, or “overweight”). The results are shown in the two-way table below, broken down by gender.

1. What percent of women said that they felt overweight?

2. What percent of overweight people were women?

3. The two-way table above has a chi-squared statistic of $\chi^2 = 226.6$. How many degrees of freedom does the table have and what is the corresponding p-value?

4. Is the association between gender and perceived body weight statistically significant?

5. A study from the 1990s looked at whether the anti-retroviral drug AZT can help prevent pregnant women with HIV from passing the virus on to their children. The mom’s were randomly assigned to receive either AZT or a placebo, and the results are shown in the two-way table below.

   	HIV-positive baby	HIV-negative baby
   AZT	13	167
   Placebo	40	143

   This table has $\chi^2 = 15.6$. Is this strong evidence that AZT works better than a placebo?

Wed, Dec 3

Today we talked some more about the $\chi^2$-test for association. We mentioned that the $\chi^2$-distribution has these features:

• Shape: Skewed right
• Center: The mean $\mu$ is the degrees of freedom.

The assumptions for the $\chi^2$-test are:

1. No Bias: Data should come from a simple random sample.
2. Normality: Sample should have at least 5 individuals in each cell of the two-way table.

We did the following example where the $\chi^2$-test is inconclusive:

1. The 2008 General Social Survey asked people if they were “very happy”, “pretty happy”, or “not too happy” with their lives. Here are the results broken down by gender.

   	Female	Male
   Very Happy	271	328
   Pretty Happy	513	587
   Not Too Happy	142	174

   This table has $\chi^2 = 0.46$. Is there a statistically significant association between the two variables in this two way table? What are the two variables?

• Workshop: Chi-squared test

Fri, Dec 5

Class was canceled because of snow.

Mon, Dec 8

Today we went over answers to the review questions for the final exam.