Statistics Notes

Math 121 - Spring 2026

• Class Notes
• Schedule & Syllabus
• Software & Tables

Week 1 Notes

Mon, Jan 12

Today we covered data tables, individuals, and variables. We also talked about the difference between categorical and quantitative variables.

• Example: Class data

1. We looked at a case of a nurse who was accused of killing patients at the hospital where she worked for 18 months. One piece of evidence against her was that 40 patients died during the shifts when she worked, but only 34 died during shifts when she wasn’t working. If this evidence came from a date table, what would be the most natural individuals (rows) & variables (columns) for that table?

• Example: Accident Fatalities by State (source: CDC)

2. In the data table in the example above, who or what are the individuals? What are the variables and which are quantitative and which are categorical?

3. If we want to compare states to see which are safer, why is it better to compare the rates instead of the total fatalities?

4. What is wrong with this student’s answer to the previous question?

Rates are better because they are more precise and easier to understand.

I like this incorrect answer because it is a perfect example of bullshit. This student doesn’t know the answer so they are trying to write something that sounds good and earns partial credit. Try to avoid writing bullshit. If you catch yourself writing B.S. on one of my quizzes or tests, then you can be sure that you a missing a really simple idea and you should see if you can figure out what it is.

Wed, Jan 14

We talked briefly about making bar charts for categorical data.

1. Exercise 2.21

Then we introduced stem & leaf plots (stemplots) and histograms for quantitative data. We started by making a stemplot and a histogram for the weights of the students in the class. We also talked about how to tell if data is skewed left or skewed right.

• Example: US Household Income (2023)

2. Can you think of a distribution that is skewed left?

3. Why isn’t this bar graph from the book a histogram?

Then we did this workshop:

• Workshop: Histograms & stemplots

We finished by reviewing the mean and the median.

Fri, Jan 16

We introduced the five number summary and box-and-whisker plots (boxplots). We also talked about the interquartile range (IQR) and how to use the $1.5 \times \text{IQR}$ rule to determine if data is an outlier.

We started with this simple example:

1. An 8 man crew team actually includes 9 men, the 8 rowers and one coxswain. Suppose the weights (in pounds) of the 9 men on a team are as follows:

    120  180  185  200  210  210  215  215  215

   Find the 5-number summary and draw a box-and-whisker plot for this data. Is the coxswain who weighs 120 lbs. an outlier?

• Workshop: Boxplots

Week 2 Notes

Wed, Jan 21

Today we talked about robust statistics such as the median and IQR that are not affected by outliers and skew. We also introduced the standard deviation. We did this one example of a standard deviation calculation by hand, but you won’t ever have to do that again in this class.

1. 11 students just completed a nursing program. Here is the number of years it took each student to complete the program. Find the standard deviation of these numbers.

    3  3  3  3  4  4  4  4  5  5  6

From now on we will just use software to find standard deviation. In a spreadsheet (Excel or Google Sheets) you can use the =STDEV() function.

2. Which of the following data sets has the largest standard deviation?

   1. 1000, 998, 1005
   2. 8, 10, 15, 20, 22, 27
   3. 30, 60, 90

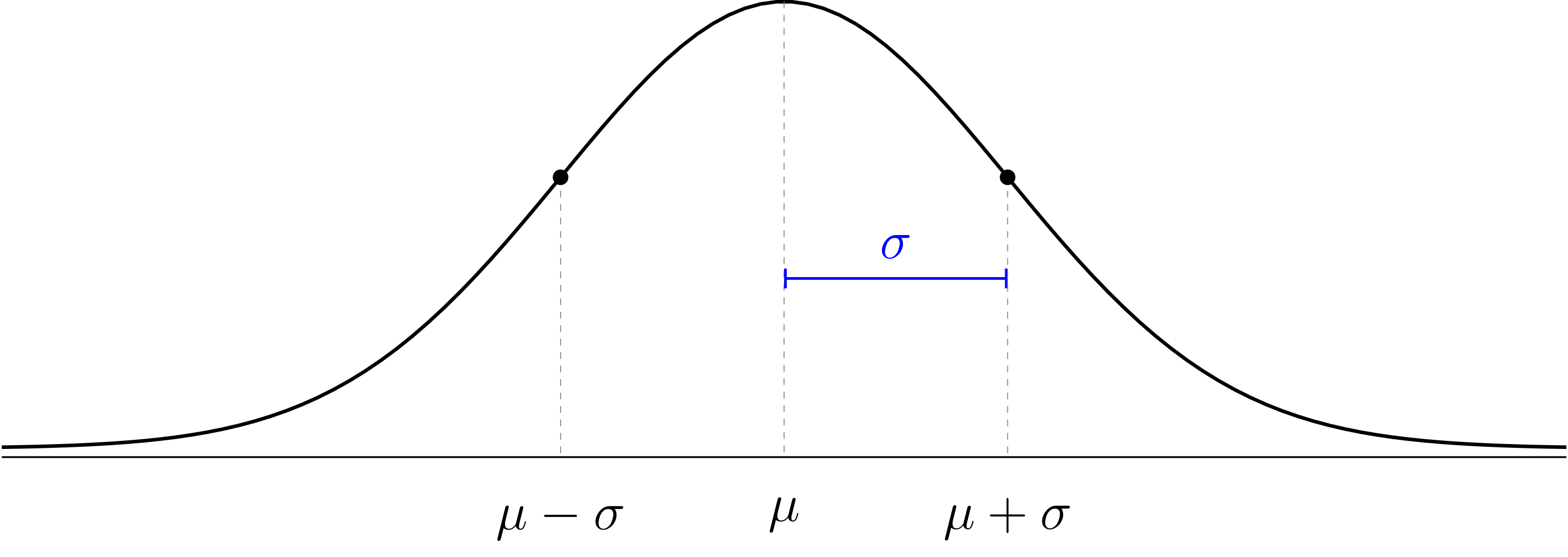
We finished by looking at some examples of histograms that have a shape that looks roughly like a bell. This is a very common pattern in nature that is called the normal distribution.

• Example: Heights of men in the USA
• Example: Annual rainfall in Farmville, VA

The normal distribution is a mathematical model for data with a histogram that is shaped like a bell. The model has the following features:

1. It is symmetric (left & right tails are same size)
2. The mean ($\mu$) is the same as the median.
3. It has two inflection points (the two steepest points on the curve)
4. The distance from the mean to either inflection point is the standard deviation ($\sigma$).
   
5. The two numbers $\mu$ and $\sigma$ completely describe the model.

The normal distribution is a theoretical model that doesn’t have to perfectly match the data to be useful. We use Greek letters $\mu$ and $\sigma$ for the theoretical mean and standard deviation of the normal distribution to distinguish them from the sample mean $\bar{x}$ and standard deviation $s$ of our data which probably won’t follow the theoretical model perfectly.

Fri, Jan 23

We talked about z-values and the 68-95-99.7 rule.

• Workshop: Normal distributions

We also did these exercises before the workshop.

1. In 2020, Farmville got 61 inches of rain total (making 2020 the second wettest year on record). How many standard deviations is this above average?

2. The average high temperature in Anchorage, AK in January is 21 degrees Fahrenheit, with standard deviation 10. The average high temperature in Honolulu, HI in January is 80°F with σ = 8°F. In which city would it be more unusual to have a high temperature of 57°F in January?

Week 3 Notes

Wed, Jan 27

We introduced how to find percentages on a normal distribution for locations that aren’t exactly one, two, or three standard deviations away from the mean. I strongly recommend downloading the Probability Distributions app (android version, iOS version) for your phone.

We talked about how to use the app to solve the following types of problem:

1. (Percent below) SAT verbal scores are roughly normally distributed with mean μ = 500, and σ = 100. Estimate the percentile of a student with a 560 verbal score.

2. (Percent above) What percent of students get above a 560 verbal score on the SATs?

3. (Percent between) What percent of men are between 6 and 6 and a half feet tall?

4. (Percent to locations) What is the height of a man in the 25th percentile?

We also talked about the shorthand notation $$P(72 < X < 78)$$ which literally means “the probability that the outcome X is between 72 and 78”. Then we did this workshop.

• Workshop: Normal distributions 2

Fri, Jan 30

We introduced scatterplots and correlation coefficients with these examples:

• Blood Alcohol Content vs. Number of Beers
• Marriage ages
• Example R values
• Guess the correlation

1. What would the correlation between husband and wife ages be in a country where every man married a woman exactly 10 years older? What if every man married a woman exactly half his age?

Important concept: correlation does not change if you change the units or apply a simple linear transformation to the axes. Correlation just measures the strength of the linear trend in the scatterplot.

Another thing to know about the correlation coefficient is that it only measures the strength of a linear trend. The correlation coefficient is not as useful when a scatterplot has a clearly visible nonlinear trend.

After we finished that, we talked about explanatory & response variables (see section 1.2.4 in the book).

2. An article in the journal Pediatrics found an association between the amount of acetaminophen (Tylenol) taken by pregnant mothers and ADHD symptoms in their children later in life. What are the variables? Which is explanatory and which is response?

3. Does your favorite team have a home field advantage? If you wanted to answer this question, you could track the following two variables for each game your team plays: Did your team win or lose, and was it a home game or away. Which of these variables is explanatory and which is response?

Week 4 Notes

Mon, Feb 2

We talked about least squares regression. The least squares regression line has these features:

1. Slope $m = R \frac{s_y}{s_x}$
2. Point $(\bar{x}, \bar{y})$
3. y-Intercept $b = \bar{y} - m \bar{x}$

You won’t have to calculate the correlation $R$ or the standard deviations $s_y$ and $s_x$, but you might have to use them to find the formula for a regression line.

We looked at these examples:

• Blood Alcohol Content vs. Number of Beers
• Marriage ages
• Midterm exam grades

Keep in mind that regression lines have two important applications.

• Make predictions about average y-values at different x-values.
• The slope is the rate of change.

It is important to be able to describe the units of the slope.

1. What are the units of the slope of the regression line for predicting BAC from the number of beers someone drinks?

2. What are the units of the slope for predicting someone’s weight from their height?

We also introduced the following concepts.

Wed, Feb 4

• Workshop: Lightning fatalities

Before the workshop, we started with this warm-up exercise.

1. A sample of 20 college students looked at the relationship between foot print length (cm) and height (in). The sample had the following statistics: $$\bar{x} = 28.5 \text{ cm}, ~\bar{y} = 67.75 \text{ in}, ~ s_x = 3.45 \text{ cm}, ~ s_y = 5.0 \text{ in}, ~ R = 0.71$$

   1. Find the slope of the regression line to predict height ($y$) based on footprint length ($x$). Include the units and briefly explain what it means.
      
   2. If a footprint was 30 cm long, how tall would you predict the subject was?

Fri, Feb 6

We talked about the difference between samples and populations. The central problem of statistics is to use sample statistics to answer questions about population parameters.

We looked at an example of sampling from the Gettysburg address, and we talked about the central problem of statistics: How can you answer questions about the population using samples?

The reason this is hard is because sample statistics usually don’t match the true population parameter. There are two reasons why:

• Bias: systematic error (each source has error in a particular direction)
• Random error: non-systematic error

We looked at this case study:

• Gallup polling & sample bias

Week 5 Notes

Mon, Feb 9

We did this workshop.

• Workshop: Random error versus bias

Week 6 Notes

Mon, Feb 16

One of the hardest problems in statistics is to prove causation. Here is a diagram that illustrates the problem.

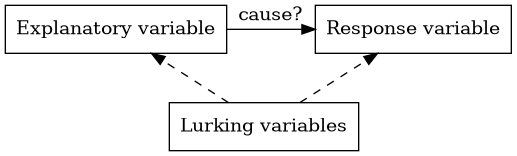
The explanatory variable might be the cause of a change in the response variable. But we have to watch out for other variables that aren’t part of the study called lurking variables. When researchers take a variable into account in a study, we say it is controlled.

We say that correlation is not causation because you can’t assume that there is a cause and effect relationship between two variables just because they are strongly associated. The association might be caused by lurking variables or the causal relationship might go in the opposite direction of what you expect.

We looked at these examples.

1. A study tried determine whether cellphones cause brain cancer. The researchers interviewed 469 brain cancer patients about their cellphone use between 1994 and 1998. They also interviewed 469 other hospital patients (without brain cancer) who had the same ages, genders, and races as the brain cancer patients.

   1. What was the explanatory variable?
   2. What was the response variable?
   3. Which variables were controlled?
   4. Was this an experiment or an observational study?
   5. Are there any possible lurking variables?

2. In 1954, the polio vaccine trials were one of the largest randomized controlled experiments ever conducted. Here were the results.

   1. What was the explanatory variable?
   2. What was the response variable?
   3. This was an experiment because it had a treatment variable. What was that?
   4. Which variables were controlled?
   5. Why don’t we have to worry about lurking variables?

We talked about why the polio vaccine trials were double blind and what that means.

Here is one more example we didn’t have time for:

3. Do magnetic bracelets work to help with arthritis pain?

   1. What is the explanatory variable?
   2. What is the response variable?
   3. How hard would it be to design a randomized controlled experiment to answer the question above?

We finished by talking about anecdotal evidence.

Wed, Feb 18

Today we introduced probability models which always have two parts:

1. A list of possible outcomes called a sample space.
2. A probability function $P(E)$ that gives the probability for any subset $E$ of the sample space.

A subset of the sample space is called an event. We already intuitively know lots of probability models, for example we described the following probability models:

1. Flip a coin.

2. Roll a six-sided die.

3. If you roll a six-sided die, what is $P(\text{result at least 5})?$

4. The proportion of people in the US with each of the four blood types is shown in the table below.

   Type	O	A	B	AB
   Proportion	0.45	0.40	0.11	?

   What is $P(\text{Type AB})?$

• Workshop: Probability models

Fri, Feb 20

Today we talked about the multiplication and addition rules for probability. We also talked about independent events and conditional probability. We started with these examples.

1. If you roll two six-sided dice, the results are independent. What is the probability that both dice land on a six?

2. Suppose you shuffle a deck of 52 playing cards and then draw two cards from the top. Find
   1. $P(\text{First card is an ace})$
   2. $P(\text{Second card is an ace } | \text{ first is an ace})$
   3. $P(\text{Second card is an ace } | \text{ first is not an ace})$

Then we did this workshop:

• Workshop: Basic probability rules

Week 7 Notes

Mon, Feb 23

Today we talked about weighted averages. To find a weighted average:

1. Multiply each number by its weight.
2. Add the results.

We did this workshop.

• Workshop: Expected value & weighted averages

Before that, we did some examples.

1. Calculate the final grade of a student who gets an 80 quiz average, 72 midterm average, 95 project average, and an 89 on the final exam.

2. Eleven nursing students graduated from a nursing program. Four students completed the program in 3 years, four took 4 years, two took 5 years, and one student took 6 years to graduate. Express the average time to complete the program as a weighted average.

The expected value (also known as the theoretical average) is the weighted average of the outcomes in a probability model, using the probabilities as the weights.

3. In roulette there is a wheel with 38 slots. There are 18 red slot, 18 black slots and 2 green slots. When you spin the wheel, you can bet that the ball will land on a black slot. If you bet $1, and the ball lands on black, then you win $2, otherwise you win nothing. What is the expected value for this bet?

Wed, Feb 25

We started with this warm-up problem.

1. Last time we calculated the expected value if you play roulette and bet $1 on a color like black. If you bet $1 on a number, like 7, then you only have a 1/38 chance of winning, but you get $36 if you win. Find the expected value for this bet.

After that we introduced the binomial distribution which is the distribution of the possible number of successes if you do N independent random trials that each have a probability p of a success.

• Example: Binomial distribution

2. Suppose you play 100 games of roulette and bet on 7 every time. Use the binomial distribution app to find the probability that you win more money than you lose.

3. What about playing 100 games and betting on black every time? Which is a better strategy?

The binomial distribution is an example of a discrete distribution which means that there are only finitely many possible outcomes between any two values. The normal distribution is an example of a continuous distribution which can have an infinite range of possible outcomes between two values.

Every probability distribution can be described by three things:

• Shape - is it shaped like a bell, or skewed, or something even more complicated?
• Center - the theoretical average $\mu$ (i.e., the expected value)
• Spread - the theoretical standard deviation $\sigma$

We usually won’t calculate the theoretical standard deviation of a probability model by hand. But, there are nice formulas for the theoretical mean and standard deviation of a binomial distribution.

We finished by talking about the trade-off between risk ($\sigma$) versus expected returns ($\mu$) when investing.

Fri, Feb 27

Suppose we are trying to study a large population with mean $\mu$ and standard deviation $\sigma$. If we take a random sample, the sample mean $\bar{x}$ is a random variable and its probability distribution is called the sampling distribution of $\bar{x}$. Assuming that the population is large and our sample is a simple random sample, the sampling distribution always has the following features:

Examples of sampling distributions.

• Gettysburg Address words
• Weights of adults
• NFL kickoffs

1. Every week in the Fall there are about 15 NFL games. In each game, there are about 13 kickoffs, on average. So we can estimate that there might be about 200 kickoffs in one week of NFL games. Those 200 kickoffs would be a reasonably random sample of all NFL kickoffs. Describe the sampling distribution of the average kickoff distance.

2. The average American weighs $\mu = 170$ lbs. with a standard deviation of $\sigma = 40$ lbs. If an airplane is designed to seat 22 passengers, what is the probability that the combined weight of the passengers would be greater than 4,000 lbs? Hint: This is the same as finding $P(\bar{x} > 181.8)$

Week 8 Notes

Mon, Mar 2

We started with this warm-up problem which is a review of the things we talked about last week.

1. Annual rainfall totals in Farmville are approximately normal with mean 44 inches and standard deviation 7 inches.

   1. How likely is a year with more than 50 inches of rain?

   2. How likely is a whole decade with average annual rainfall over 50 inches?

Then we talked about sample proportions which are denoted $\hat{p}$ and can be found using the formula $$\hat{p} = \frac{\text{ number of "successes" }}{\text{ sample size }}.$$ In a SRS from a large population, $\hat{p}$ is random with a sampling distribution that has the following features.

We did the following exercises in class.

1. This semester, 7 out of 25 students in my statistics class were born in VA. Is $\frac{7}{25}$ a statistic or a parameter? Should you denote it as $p$ or $\hat{p}$?

2. In the United States about 7.2% of people have type O-negative blood, so they are universal donors. Is 7.2% a parameter ($p$) or a statistic ($\hat{p}$)?

3. If a hospital has $N = 900$ patients, describe the sampling distribution for the proportion of patients who are universal donors.

4. Find the probability that $P(\hat{p}_{\text{universal donor}} > 8\%)$.

5. About one third of American households have a pet cat. If you randomly select $N = 50$ households, describe the sampling distribution for the proportion that have a pet cat.

6. According to a 2006 study of 80,000 households, 31.6% have a pet cat. Is 31.6% a statistic or a parameter? Would it be better to use the symbol $\hat{p}$ or $p$ to represent it?

Wed, Mar 4

Today we talked about confidence intervals for proportions. These are based on a simple idea: there is a 95% chance that the sample proportion $\hat{p}$ is no more than 2 standard deviations away from the true population proportion $p$.

The variable $z^*$ is called the critical z-value is determined by the desired confidence level. Here are some common choices.

In order to trust a confidence interval, you need these two assumptions to hold:

1. No Bias. The data should come from a simple random sample to avoid bias.

2. Normality. The sample size must be large enough for $\hat{p}$ to be normally distributed. A rule of thumb (the success-failure condition) is that you should have at least 15 “successes” and 15 “failures” in the sample.

We did the following examples in class.

1. In our class 7 out of 25 students were born in VA. Use the 95% confidence interval formula to estimate the percent of all HSC students that were born in VA.

2. In 2004 the General Social Survey found 304 out 977 Americans always felt rushed. Find the 90% confidence interval for the proportion of Americans who always feel rushed.

3. What are we 90% sure is true about the confidence interval we found? Only one of the following is the correct answer. Which is it?

   1. 90% of Americans are in the interval.
   2. 90% of future samples will have results in the interval.
   3. 90% sure that the population proportion is in the interval.
   4. 90% sure that the sample proportion is in the interval.

A confidence interval has two parts: a best guess estimate (or point estimate) before the plus/minus symbol, and a margin of error after the $\pm$ symbol.

4. (Subsection 5.2.4 from OpenIntro Stats) In 2014 an American Doctor who had been working in Africa was diagnosed with Ebola. He was flown back to New York city to be treated. This was controversial at the time because Ebola is a very contagious and dangerous disease. A Marist poll of 1042 NY adults found that 82% would support a mandatory 3-week quarantine for anyone who has had contact with an Ebola patient. What is the margin of error for this poll?

Fri, Mar 6

Last time we introduced confidence intervals for proportions. Today we did some more examples related to confidence intervals.

1. A 2017 Gallop survey of 1,011 American adults found that 38% believe that God created man in his present form. Find a 95% confidence interval to estimate the percent of all Americans who share this belief.

2. About one third of American households have a pet cat. How large of a sample would be need if you wanted to make a 95% confidence interval with a margin of error less than 1% for the percent of households with a pet cat?

3. One of our first examples of sampling was the Literary Digest magazine poll from the 1936 presidential election. They had a huge sample with 2.4 million responses. In that sample, 62% supported Alfred Landon (R) over FDR (D). What is the margin of error for a 99% confidence interval with this data?

4. How is it possible that the margin of error could be so small if the poll was so wrong?

Week 9 Notes

Week 10 Notes

Week 11 Notes

Week 12 Notes

Week 13 Notes

Week 14 Notes