| Day | Section | Topic |
|---|---|---|
| Mon, Jan 13 | 1.3 | Proof techniques |
| Wed, Jan 15 | 2.1 - 2.2 | Notation & encodings |
| Fri, Jan 17 | 3.1 - 3.7 | Boolean circuits |
Today we talked about proof techniques, particularly proof by induction. We looked at these two examples:
The second example had to do with the famous Tower’s of Hanoi puzzle( see https://youtu.be/SMleU0oeGLg).
You can also translate many induction arguments into recursive algorithms.
Write a Python function sublists(A) that inputs a
list A and returns a list containing every sublist of
A.
We did this in class and we came up with something like this:
def sublists(A):
if len(A) == 0:
return [A]
last = A[-1]
B = A[0:-1]
sublists_without_last = sublists(other_elements)
sublists_with_last = [s + [last] for s in sublists_without_last]
return sublists_without_last + sublists_with_lastSuppose you have three stack variables (implemented as Python lists):
stack1 = [10 - k for k in range(10)]
stack2 = []
stack3 = []Write a function
move_disks(n, start_stack, temp_stack, final_stack) that
recursively moves n disks from the start_stack to the
final stack.
Today we reviewed mathematical notation, including some new notation we will be using. We defined alphabets which are sets of symbols we can use to represent things. The most common alphabet in computer science is the binary alphabet . We use the notation to denote the set of all possible finite length strings constructed from .
A set can be represented or encoded using an alphabet if there is a 1-to-1 function .
Theorem. Any countable set can be encoded with a 1-to-1 function .
We discussed specific encodings such as how to encode the integers and the rationals .
We also observed another fact:
Theorem. If we can encode a set using , then we can encode tuples in using .
At the end we considered the set which you can think of as the set of all infinitely long strings of zeros and ones. We finished by proving
Theorem. There is no one-to-one function from into .
A corollary of this theorem is that is uncountable.
We talked about Boolean circuits which are formed by AND, OR, and NOT gates. These can be used to implement any Boolean expression formed by the (AND), (OR), and (NOT) operators.

Write a Boolean expression that takes three Boolean inputs,
and returns true if
are all the same, and false otherwise.
Show that you can construct the function IF x THEN y ELSE z for any Boolean inputs x, y, z using AND, OR, and NOT gates.
Use mathematical induction (and the previous result) to prove the following:
Theorem. Every function can be represented by a Boolean circuit.
We say that the Boolean operations (, , ) are a universal set of operations since every Boolean function on can be constructed using those operations.
We finished by talking about how the NAND operation is universal all by itself. Using just NAND gates, you can construct any Boolean function on .
Theorem. Every function can be represented using NAND operations.
Show that you can use a NAND gate to implement a NOT gate.
Show that you can use two NAND gates to implement an AND gate.
Use a truth table to confirm that
(NOT x) NAND (NOT y) is equivalent to
x OR y.
| Day | Section | Topic |
|---|---|---|
| Mon, Jan 20 | MLK day, no class | |
| Wed, Jan 22 | Impossible computer programs | |
| Fri, Jan 24 | 2.1 | Intro to finite automata |
Last time we saw that some functions
cannot be computed by a computer program. We saw two proofs that seemed
very different. One used a cardinality argument and the other used proof
by contradiction to show that the program
check_if_program_returns_one() is impossible. It turns out
that both proofs are actually closely related.
Suppose we make a list of all possible programs on the left column of an infinite table, with a list of all possible input strings at the top of the table. The values in the body of the table are the output of each program on each input (including the possibility that there is no output). The table might look like this:
| Input 1 | Input 2 | Input 3 | ||
|---|---|---|---|---|
| Program 1 | 1 | 1 | 1 | |
| Program 2 | 0 | 0 | na | |
| Program 3 | 0 | na | 1 | |
We can construct a function
that cannot correspond to any program by using the same diagonalization
argument that proves that there are uncountably many infinite binary
sequences. That’s essentially what we did when we tried to construct the
function check_if_program_returns_one() last time. We
created a function reverse_check() that corresponds to
reversing the values on the main diagonal of the table above. So we were
using a diagonalization argument, which is the same
argument used to prove that there are uncountably many functions
.
After that, we introduced finite automata. We started with this example: An automatic door at a grocery store has sensors on the front and rear. It opens if the sensor on the front is active. It won’t close until neither of the sensors are active. You can model this with the following state diagram:
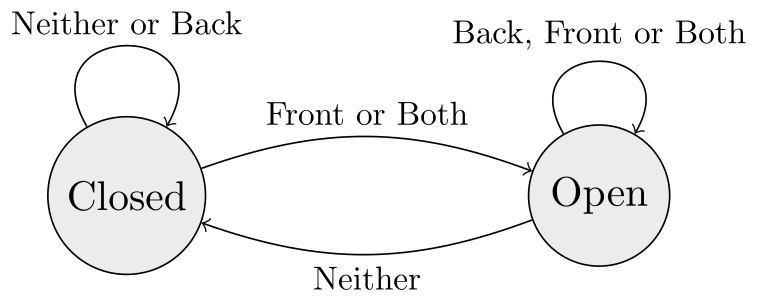
This is an example of a finite state machine, also known as a deterministic finite automata (DFA).
Definition. A deterministic finite automata (DFA) consists of
What are the sets and for the automatic door example above?
Make a table showing the values of the transition function for the automatic door.
An automatic toll booth accepts nickles, dimes, and quarters. The gate won’t open until it receives 25 cents. Draw a state diagram for the toll booth. What are the sets and ?
A combination lock (like the ones at the campus post office) can be modeled as a finite state machine. What are the states and what are the input signals?
Describe a DFA that can compute the function which returns 1 when the input string has an odd number of 1’s and 0 otherwise.
| Day | Section | Topic |
|---|---|---|
| Mon, Jan 27 | 2.2 - 2.3 | Regular languages |
| Wed, Jan 29 | 2.4 | Nondeterministic finite automata |
| Fri, Jan 31 | 2.6 | NFAs and regular languages |
Today we started with these questions about DFAs:
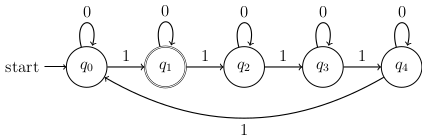
Definition. For any finite alphabet , a language is a subset of . A language is regular if there is a DFA such that .
Conceptually, when we think about a DFA, we understand that it can do two things:
It’s important to understand that these two interpretations of what a DFA does are equivalent, because there is a simple bijection between the set of all possible languages (the power set of ) and the set of all possible functions .
Our solution ended up involving the indicator function for a set , where
We started by constructing some more examples of DFAs.
Find a DFA that computes whether a binary string ends with 011. (This is similar, but not the same as a DFA we constructed last time).
How many states would a DFA need if you wanted to check whether a binary string has a 1 in the third position from the last?
Then we talked about these properties of regular languages.
Theorem (Finite languages are regular). If is a finite alphabet, then any finite is a regular language.
Theorem (Closure properties of regular languages). Let be regular languages. Then
We say that the set of regular languages over is closed under the three operations: union, concatentation, and Kleene-star.
We proved the first part of the theorem above (regular languages are closed under unions) in class by thinking about how to construct a new DFA that accepts using DFAs and that accept and respectively. To prove this, we answered these questions:
If the machine is built by running both and simultaneously, what are the possible states of ?
What are the initial states for ?
What is the transition function for ?
What are the accepting states of ?
We started by asking whether regular languages are closed under intersections. Can we adapt the proof we gave last time for unions to intersections?
Yes, regularly languages are closed under intersections. The proof is almost exactly the same as the proof for unions, the only difference is that the DFA to recognize has final states while the DFA to recognize has final states , that is, any pair of states from where at least one of the two is final.
To prove that regular languages are closed under concatenation, we introduced a new idea: non-deterministic finite automata (NFAs).
We looked at this example:
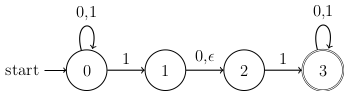
An NFA can have more than one arrow exiting a state with the same input. When that happens, the machine splits into multiple copies, one for each possible next state.
If an NFA enters a state that has exiting arrows labeled with , then the NFA immediately splits into multiple copies, one where the current state stays the same, and one where the current state moves along each branch labeled . This can happen several times, if there is a sequence of branches labeled .
If there is no arrow leaving a state for a given input signal, that means that the current copy of the machine is a dead end and it does not need to be continued.
The NFA accepts a string if any of the parallel computations is in an accepting state after the string is read. We answered these questions:
Which states are active at each step as we read the input string 01010?
Does this NFA accept the string 01010?
Describe the set of all strings in that this NFA will accept.
Here is the technical definition of an NFA.
Definition. A non-deterministic finite automata (NFA) consists of
The only change from the definition of a DFA is that the transition function for an NFA can return a set of states at each step (including, possibly, the empty set). Think of these multivalued transitions as creating multiple branching computations that run in parallel. If the transition function returns the empty set, that means that that branch of the parallel computation is a dead end and does not continue.
Let be regular languages recognized by DFAs and respectively. Describe an NFA that uses the and to check if a string is in the union . Note that every DFA is an NFA that has a transition function that only ever returns a single state at a time.
Describe an NFA that can check whether or not the 3rd to last digit of a binary string is 1 using fewer states than the DFA we described last time. Hint: What if the NFA “guesses” every time it sees a 1 that that might be the third to last entry. What should it’s states be from that point on?
| Day | Section | Topic |
|---|---|---|
| Mon, Feb 3 | 2.5 | NFAs and DFAs are equivalent |
| Wed, Feb 5 | 2.7 | Regular expressions |
| Fri, Feb 7 | 2.8 | Regular expressions and languages |
Today we continued talking about NFAs. We’ve been following the textbook by Meshwari & Smid pretty closely this week, so I recommend reading skimming Section 2.6 which is what we covered today.
We described an NFA that recognizes the concatentation of two regular languages by running DFAs and in parallel. We answer these questions about the NFA:
We also described an NFA that recognizes the Kleene star of a regular language. The idea is similar to the previous construction, but you need a way to accept the empty string (if it isn’t part of ).
To complete the proof that regular languages are closed under these two operations, we need to prove this:
Theorem (Equivalence of NFAs and DFAs). If there is an NFA that recognizes a language , then there is a DFA that also recognizes .
The proof is surprisingly simple. An NFA with states , transition function can be turned into a DFA that has states and transition function .
Describe specifically what returns for any subset using .
If denotes the accepting states of the NFA, then what are the corresponding accepting states of the DFA?
If is the initial state of the NFA, what is the initial state of the DFA?
We applied the idea of this proof to Exercise 5 from Homework 3.
We introduced regular expressions (regex).
Definition. A regular expression over an alphabet is a string with symbols from the extended alphabet that has one of the following forms:
We also accept the empty set and the empty string as regular expressions.
Regular expressions are used to match sets of strings (i.e., languages over ).
Describe what the following regular expressions represent:
(0|1)0*Σ*1Σ*(0|1)*Write a regular expression that recognizes the base-10 decimal form of any integer that is a multiple of 5.
Most programming languages use Perl compatible regular expressions which have several additional features to make it easier to work with regular expressions. Here are some examples we talked about in class.
| Special Symbols | |
|---|---|
\s
|
whitespace (tabs, spaces, etc.) |
\w
|
alphanumeric (letters & digits) |
\d
|
digits (0-9) |
.
|
wildcard matches any single character |
\
|
escape (for special characters) |
|
|
||||||||||||||||
Here is a simple Python regex example:
import re
s = "My pet dog likes to go to the park."
expr = "pet\s(dog|cat|bird)"
match = re.search(expr, s)
print(match)Write a regular expression that would match any e-mail address of
the form name@domain.extension.
Find a regular expression over the alphabet that matches all strings that start with a 1, end with a 1, and have an even number of zeros between.
We stated, but did not prove the following theorem.
Theorem (Equivalence of regular expressions and regular languages). A language is regular if and only if there is a regular expression that describes it.
(ab|a)*. Use the ideas from the previous classes
about how to build NFAs to find the union, concatenation, and Kleene
star of languages.Today we talked about the proof of the theorem from last time that regular languages and regular expressions are equivalent. One direction is easy: every language described by a regular expression is regular. This is because we already know that regular languages are closed under the union, concatenation, and Kleene-star operations and we also know that any finite set of strings is a regular language.
Therefore, we should be able to solve this example, which we didn’t have time for on Wednesday.
(ab|a)*. Use the ideas from the previous classes
about how to build NFAs to find the union, concatenation, and Kleene
star of languages.To prove the converse, we described an algorithm for converting NFAs to regular expressions. Note that the Maheshwwari & Smid textbook describes a different approach to convert an NFA into a regular expression in Section 2.8. Our approach is to use a generalized NFA:
Definition. A generalized non-deterministic finite automata (GNFA) is just like an NFA, except for the following changes:
There is only one accept state and it is not the start state.
No transitions enter the start state or leave the accept state.
Transitions can be triggered by input strings that match a regex (not just single symbols).
To finish the proof, we make two observations:
First, you can convert any NFA to a GNFA by adding a special start state that has an epsilon transition to the original start state and a new accept state that has an epsilon transition from any old final state.
Second, if you have a GNFA with states, there is an equivalent GNFA with states, because you can remove any state (other than the initial and final states) and replace incoming/outgoing transitions with transitions described by a regex.
We did the following example to illustrate.
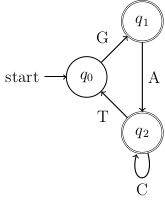
We finished by talking about languages which are not regular. One simple language that is not regular is the following:
| Day | Section | Topic |
|---|---|---|
| Mon, Feb 10 | 2.9 | Non-regular languages & the pumping lemma |
| Wed, Feb 12 | 2.9 | More non-regular languages |
| Fri, Feb 14 | Review |
Theorem (Pumping Lemma). If is a regular langauage, then has a length (called the pumping length of ) such that if a string is longer than , then where are substrings such that
Here is a picture that helps to understand what is going on. It also gives a clue about why this theorem is true.

The proof is really simple. If a finite state machine reads a long enough string, eventually it has to loop back to the same state twice. The input signals that caused the machine to take that loop make up the substring in the theorem.
The pumping lemma is a useful tool to prove that some languages are not regular. You can use the pumping lemma to give a proof by contradiction. Be careful, the pumping lemma cannot be used to prove that a language is regular.
Steps to prove a language is not regular
Temporarily assume the language is regular and has pumping length .
Try to construct a string in so that:
If you can’t pump the string, that contradicts the pumping lemma, so can’t be regular.
We applied this technique to prove that the following languages are not regular.
Here is a nice meme proof using the pumping lemma from Barak textbook.
Today we looked at more examples of regular and non-regular languages.
.
.
The converse of the pumping lemma is not true. So you can’t use the pumping lemma to prove that a language is regular. In fact, here is a language that is non-regular, but every string in the language is pump-able!
Explain why there is a pumping number (in fact works) such that any string can be “pumped”.
Despite this, explain why is not a regular language. Hint: if there was a DFA that recognizes , what other DFAs could you construct?
Many programming languages, including Python & Javascript allow
backreferences to previous groups in a regular expression. A group is a
part of the regular expression inside parentheses. The special symbol
\1 refers to anything matched by the first group in the
regular expression. Similarly \2 refers back to anything
matched by the second group, and so on. For example: the regular
expression "(\w\w*) \1" would match any repeated word like
“word word” or “dog dog”. I tried to demonstrate this in class, but
I got tripped up because Python requires the regular expression to be
entered as a raw
string.
import re
regex = r"(\w\w*) \1" # need the r before the quotes to indicate that this is a raw string
print(re.search(regex, "Did I type the the same word twice?"))Today we went over some of the problems from homework 4 and the midterm 1 review problems.
| Day | Section | Topic |
|---|---|---|
| Mon, Feb 17 | Midterm 1 | |
| Wed, Feb 19 | 3.1 - 3.2 | Context-free grammars |
| Fri, Feb 21 | 3.3 | Parsing and parse-trees |
Class canceled because of snow.
Today we introduced context-free grammars.
Definition. A context-free grammar (CFG) consists of
We explained how the context free grammar
S → aSb
S → εgenerates the (non-regular) language
We looked at the example of a CFG and used it to identify the parts in the formal definition.
S → <subject> <verb> <object>
<subject> → <article> <noun>
<article> → a | the
<noun> → boy | girl | dog
<verb> → runs | walks | talks
<object> → <prep> <subject>
<prep> → to |fromDraw a parse tree that shows how to derive the sentence “The boy talks to the girl.”
Find a CFG for the language of matched parentheses.
Seth suggested this CFG:
S → (S)
S → ()S
S → εThis isn’t correct, but it is a good first guess. Explain why this
grammar cannot be used to construct the string (())().
Find a context-free grammar for the language
We didn’t get to this example, but it is good practice too.
Describe how to generate the string (a + a) * a
using the context free grammar below:
<expr> → <expr> + <term> | <term>
<term> → <term> * <factor> | <factor>
<factor> → (<expr>) | aWe finished by looking at this example that gives the idea of how a programming language can be though of as a context-free language.
| Day | Section | Topic |
|---|---|---|
| Mon, Feb 24 | 3.3 | Parsing and parse-trees |
| Wed, Feb 26 | 3.8 | The pumping lemma for CFGs |
| Fri, Feb 28 | 3.5 - 3.6 | Pushdown automata |
Last time we used parse trees, but didn’t define them.
Definition (Parse Tree). Given a context free grammar and a string that can be generated by the grammar, a parse tree for the string is a labeled ordered tree with nodes labeled by elements in such that the arrows leaving a node labeled by an element in correspond to one of the rules in and the nodes labeled by elements in are terminal (no arrows leave them).
Today we looked at some more examples of Context Free Grammars. Lisp is a family of programming languages that have a particularly simple syntax. Lisps are built around S-expressions, which are defined by the following CFG rules:
S → (L) | A
L → S | S L
A → <number> | <string> | <symbol>For the variables above, S represents any S-expression,
L represents a list, and A represents an atom,
which can be a number, a string, or a symbolic expression like a
variable name or operator (among other things).
Draw a parse tree for the S-expression
(* (+ 5 6) (- 4 2)). Each node in the parse tree should be
labeled with a variable (or symbol if it is a terminal node).
Is it possible to draw a different parse tree for this expression? Why or why not?
The S-expression grammar is unambigious, every expression has only one possible parse tree. Unfortunately, many CFGs are ambiguous, i.e., they allow strings with more than one parse tree. Here is a simple example.
E → E + E
E → E * E
E → (E)
E → aa+a*a two different
ways.In some (but not all cases) it is possible to find two CFGs that
generate the same set of strings, but one is ambiguous and the other
isn’t. For example, if we change the grammar above to distinguish
between expressions that are terms (T), or factors
(F) or sums of terms (E), then we can make an
equivalent CFG that is unambiguous:
E → E + T | T
T → T * F | F
F → (E) | aWe say that a language is context-free if it can be generated by a CFG. We use the shorthand CFL to denote a context-free language.
Theorem (Regular Languages are Context-Free). Every regular language is context-free.
We’ll prove this later by showing that context-free grammars correspond to a special kind of automata with a (potentially infinte) stack called a pushdown automata. But today, we talked about how you can prove this theorem using the three operations (union, concatenation, and Kleene star) for regular expressions.
If and are both context-free languages, explain why the union is context free.
If and are both context-free languages, explain why the concatenation is context free.
Explain why the Kleene star of a CFL is context-free.
Theorem (Pumping Lemma for CFLs). If is a context-free language, then has a length (called the pumping length of ) such that if a string is longer than then where are substrings such that
This is a little more complicated than the pumping lemma for regular languages. We drew some pictures of parse trees to give an intuitive explanation for why this new pumping lemma is true (see page 126 in Maheshwari & Smid).
We started by looking at two examples:
Show that the language is context-free but not regular.
What is the pumping length for the language above?
Show that is not context-free.
We didn’t have time for this last problem, so I left it as an exercise to consider:
Today we talked about pushdown automata (PDA) which are basically just NFAs with a stack. Note that the book calls these nondeterministic pushdown automata. There are also deterministic pushdown automata, but those turn out to be more complicated, and only the nondeterministic pushdown automata are actually equivalent to CFGs. So, we will always assume that our PDAs are nondeterministic, unless specifically mentioned otherwise. We started with this example:
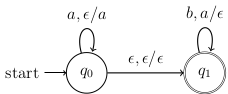
This PDA accepts the language . Notice that each arrow has three parts, for example the first loop is labeled which means you can take this loop if you read an from the input string, and pop (i.e., nothing) from the stack, and then push onto the stack. We will always use this notation (read, pop/push) for each arc.
PDAs work just like NFAs, except they have this extra rule: You only accept a string if you finish in an accepting state and the stack is empty.
Some things to note:
Since the machine is nondeterministic, you can have more than one state (and more than one stack) branching off whenever you have a choice about which arrow to take.
If you are in a state and there is no valid arrow to take, then that state dies.
Here is the formal definition.
Definition. A nondeterministic pushdown automata (PDA) consists of
Note: Some alternative definitions allow PDAs to push more than one symbol from onto the stack in one step.
We looked at these questions:
For the PDA below, describe the language that it accepts.
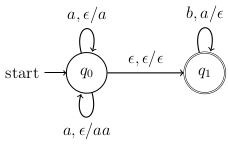
Describe an PDA that accepts the language .
Describe an PDA with just one state that accepts the language of balanced parentheses.
How many distinct PDAs with 5 states, and are possible (assuming you only push at most one variable onto the stack at each step), according to the definition?
| Day | Section | Topic |
|---|---|---|
| Mon, Mar 3 | 3.7 | Pushdown automata & context-free grammars |
| Wed, Mar 5 | 3.4 | Chomsky normal form |
| Fri, Mar 7 | 4.1 - 4.2 | Definition of Turing machines |
Today we talked about the equivalence between CFGs and PDAs.
Theorem (Equivalence of CFGs and PDAs). A language is context-free if and only if there is a pushdown automata that recognizes it.
We sketched the proof of one direction: that if you have a CFG, then there is an PDA that accepts the same language. The other direction is harder to prove, so we skipped it, but you can find the details in more advanced theory of computing textbooks.
The idea of the proof for the forward direction is to create an PDA
with three states. In state
you immediately transition to
reading nothing and push S$ on the stack (where
$ is a special symbol to mark the bottom of the stack and
S is the symbol for the start variable). Then in state
you have two different types of transitions that loop back to
:
Finally, you have a final transition to the accepting state
which involves reading nothing and popping the $ off the
stack. If you have finished reading the input when you do this, you will
accept the string.
We illustrated how this idea works using the grammar and the input
string aabbbb.
S → AB
A → aAb | ε
B → bB | bAfter this example, we talked briefly about normal forms for context-free grammars. One important normal form is the Chomsky normal form, which we will talk about next time.
For a context-free grammar , we write to denote the language generated by .
A variable in a context-free grammar is useless if there are no strings in that have a parse tree with as one of the nodes. Prove that if has any useless variables, then there is another context-free grammar that generates the same language, but does not have any useless variables.
Let be the CFG obtained by removing all useless variables from and all rules that reference those useless variables. We have to show that and both generate the same language. If , then there is a parse tree for that doesn’t contain any useless variables. Therefore the same parse tree is a parse tree for generating using , so . If , then all of the variables and rules for the parse tree to generate are also variables and rules of . Therefore which proves that .
Definition (Chomsky normal form). A context free grammar is in Chomsky normal form if all rules are in one of the following forms:
where , , and neither nor is the start variable.
One nice feature of Chomsky normal form is that it makes it easier to check whether a string can be generated by a grammar.
Definition (Equivalent grammars). Two context-free grammars are equivalent if they generate the same language.
It turns out that there is no general algorithm to check whether or not two CFGs are equivalent. But all CFGs can be converted to Chomsky normal form.
Theorem (Chomsky). Every CFG is equivalent to a CFG in Chomsky normal form.
The proof is the following algorithm to convert any CFG into Chomsky normal form.
Step 1 (Preliminaries).
Step 2 (Add terminal variables). For each terminal symbol , create a variable and add the rule . If a rule has more than one symbol in its output, then replace any terminal symbols with their corresponding terminal variables.
Step 3 (Break up long rules). For any rule of the form where , create new variables and so that you can replace the long rule with the following shorter rules:
At the end of this process your grammar will be in Chomsky normal form.
Convert the following CFG to Chomsky normal form.
S → ABa
A → aab
B → AcConvert the following CFG to Chomsky normal form.
S → aSa | A
A → abA | bExplain why the following algorithm won’t work to check if any two CFGs are equivalent:
We didn’t have time for it today, but here is one more practice example:
Convert the following CFG to Chomsky normal form.
S → ASA | A | ε
A → aa | εToday we introduced Turing machines (TMs) which are the most general model of computation that we will discuss. Turing machines are deterministic finite state machines, with an infinite tape that the machine can move along, and both read and write from. Like DFAs and PDAs, Turing machines can accept or reject an input string, but Turing machines also have a third possibility: they might loop forever and neither accept nor reject.
Here are some differences between finite automata and Turing machines:
The input string is initially written on the tape and the Turing machine is initially pointed at the first symbol of the input string.
Aside from the input string, the tape is initially filled with special blank symbols (which we’ll denote □).
The Turing machine can read and (optionally) replace one symbol on the tape at a time before moving left or right.
The TM can have both accept and reject states. When the Turing machine enters one of these states, it immediately halts and the program is complete.
A TM might loop forever without ever accepting or rejecting a string.
We looked at these examples of TMs:
Describe an algorithm that a Turing machine could implement to check if a string in is in the language . Use the tape alphabet , where you can use an to mark symbols that have been dealt with. Hint: How could you check that the first character of the string matches the first character after the equals sign?
Draw a state diagram for the Turing machine above. Use the
notation
to label transitions. The move can be either
or
,
and you can use regular expressions for the character to read. The
character to write is optional, you can move without writing
anything.
Describe an algorithm that a TM could use to accept the language Hint: Try moving from left to right, crossing out every other as you go. How will you know if there were an even number of a’s? Could you repeat the process? When should you stop?
We didn’t get to it in class, but here is a state diagram for a TM that can accept the language
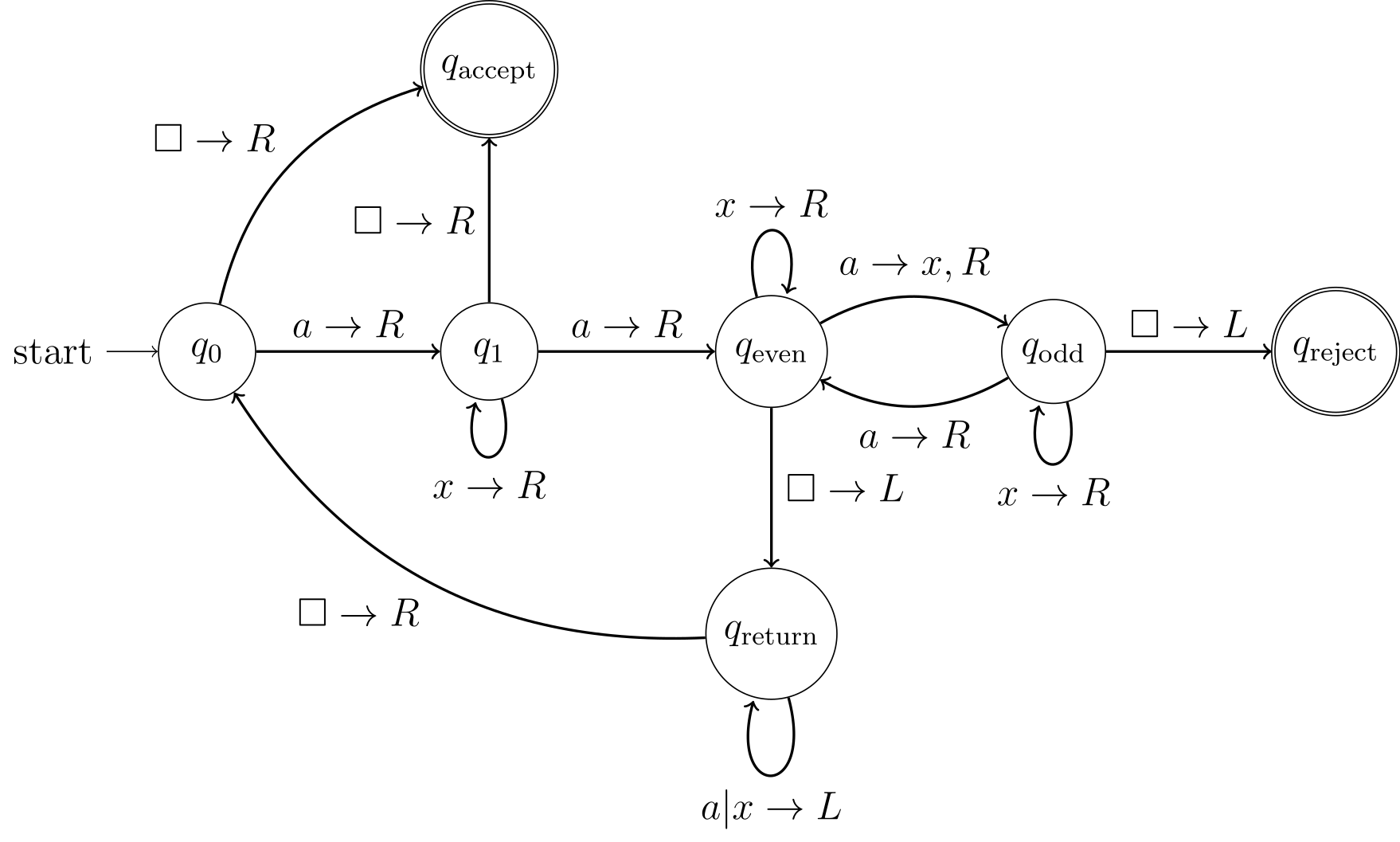
| Day | Section | Topic |
|---|---|---|
| Mon, Mar 17 | 4.2 | Turing computable functions |
| Wed, Mar 19 | 4.3 | Multi-tape Turing machines |
| Fri, Mar 21 | 4.4 | Church-Turing thesis |
Here is the formal definition of a Turing machine.
Definition. A Turing machine consists of
Because Turing machines can loop forever, there is a difference between recognizing/accepting a language and deciding a language.
Definition. A Turing machine accepts (or recognizes) a language if the set of strings that it accepts is exactly .
A Turing machine that only recognizes a language might loop forever when you give it a string that is not in .
Definition. A Turing machine decides a language if it not only recognizes , but also rejects every string that is not in .
Both of the example Turing Machines above actually decide their languages, since they will successfully reject any input that doesn’t match a valid string (they won’t get stuck looping forever without halting). We’ll see examples later of Turing machines that accept but don’t decide a language.
Another thing that Turing Machines can do is compute functions by leaving the output on the tape when it halts.
This wasn’t to hard to describe the algorithm, but it got a little complicated when we made the state diagram. Once we did that, we defined Turing computable functions.
Definition. A function is Turing computable if there is a Turing machine that halts with on the tape whenever it is given a tape with as input.
Theorem (Compostions are computable). If are both Turing computable functions, then so is the composition .
We finished by describing how this function (which comes up in the Collatz-Conjecture) is Turing computable:
Today we looked at multi-tape Turing machines.
Theorem. Any k-tape Turing machine has an equivalent single-tape Turing machine.
Proof idea. For every tape symbol of the k-tape TM, we need a “dotted” symbol and we also need a special separator symbol (#). Then we can put the contents of the k tapes onto a single tape if we add separators and dotted symbols to mark the which symbols are currently pointed to by the TM.
| # | a | ȧ | □ | a | # | ḃ | b | b | a | # | a | a | a | ȧ | # |
For each step of the k-tape TM, the 1-tape TM follows these rules:
Starting from the left, it reads the dotted symbols for each of the k-substrings. Then it returns to the leftmost position.
Then it makes a 2nd pass, updating the contents at each dotted symbol, and then moving the dot to the left or right.
If it reaches the end of a substring but needs to add a character, it first prints a special-blank then shifts every other character to the right by one, before returning to the special-blank and proceeding.
Another variation on a standard TM is a nondeterministic Turing machine (NTM). At each step, these can split into more than one possible next state. The transition function has form: The nondeterministic TM accepts a language as soon as any of its parallel versions reaches an accept state.
Theorem. Any language that can be accepted by a nondeterministic Turing machine can also be accepted by a regular Turing machine.
We talked about how you can use a 3-tape TM to used a breadth first
search through the branching possibilities of a NTM to see if any
accept.
We also talked about other things that a TM can do:
If , and are Turing computable, then so is the function
IF f(x) THEN g(x) ELSE h(x).
What about a while-loop?
while(f(x)):
x = g(x)We didn’t have time for this last example:
Can a Turing machine have a for-loop, where it repeats some
function
times? Something like this Python example where function
is applied
times?
for i in range(n):
x = f(x)We started with this example:
In mathematics, there are many algorithms, which are step-by-step procedures that can be carried out to solve problems. Prior to the work of Turing and other computer scientists, no one ever tried to define exactly what an algorithm is. It turns out to be hard to give a precise definition of an algorithm. Computer scientists have settled on the following:
Definition (Church-Turing thesis). An algorithm is a computational task that can be carried out by a Turing machine.
The idea is that Turing machines can do all of the things (like looping, and conditionals, storing variables) that we think of algorithms as doing, so we use TMs to give a precise definition for algorithms.
There are many other models of computing that can be proven to be Turing complete, that is, they can compute the same functions as Turing machines. But it is believed that there is no effective method of computation that can solve problems that Turing machines cannot solve.
We finished by discussing Hilbert’s 10th problem: Is there an algorithm to determine whether or not a multivariable polynomial with integer coefficients has an integer root? We looked at some example polynomials like
and The pair is a root for the first polynomial, since , but the second polynomial has no integer roots.
The algorithm we described will accept any polynomial that has a root. But it doesn’t reject polynomials that don’t, instead it loops forever looking for a root. It wasn’t until 1970 that Hilbert’s 10th problem was solved, when it was proved that there is no Turing machine that can decide the language of integer multivariable polynomials with integer roots. We’ll look at other examples of undecidable languages after the midterm.
| Day | Section | Topic |
|---|---|---|
| Mon, Mar 24 | Review | |
| Wed, Mar 26 | Midterm 2 | |
| Fri, Mar 28 | 5.5 - 5.7 | Universal Turing machines |
Today we reviewed context-free languages for the midterm exam. We also talked about the Chomsky hierarchy of languages.
Today we introduced universal Turing machines. We used them to consider this language:
Then we gave a diagonalization proof that Accept is not Turing decidable. Suppose there was a decider for Accept. Then we could make a table with rows for each Turing machine and columns every Turing machine encoding and entries 1 or 0 depending on whether accepts .
What would happen if we created a TM inputs any TM encoding and then does the opposite of what does on . What would do when you input into ?
Why is that a contradiction?
We finished by observed that there are only a countably infinite
number of possible Turing machines, but there is an uncountable infinite
number of languages, so there must be lots of languages that
are not decidable!
| Day | Section | Topic |
|---|---|---|
| Mon, Mar 31 | 5.1-5.3 | The halting problem & Rice’s theorem |
| Wed, Apr 2 | 6.1 | The running time of algorithms |
| Fri, Apr 4 | 6.1 | The running time of algorithms |
We started by explaining why our proof from last time that the
language Accept is undecidable was a diagonalization argument. Suppose
there were a Turing machine
(call it a decider) that can decide whether or not any
other TM will accept any string.
Imagine we make a table with columns corresponding to different Turing machine encodings and rows corresponding to different Turing machines showing the output of on each pair.
| 1 | 0 | 1 | ||
| 0 | 1 | 0 | ||
| 0 | 0 | 0 | ||
But what happens if we create a new TM that always returns the opposite of ? Why is there a contradiction if we try to look up the diagonal entry where is given itself and its encoding string as inputs?
By proving that no TM can decide the language Accept, we get the following corollary about the halting problem.
Theorem (The Halting Problem is Undecidable). The
language
is undecidable.
We gave a proof by contradiction for this theorem.
It turns out that not only is the halting problem undecidable, but lots of other questions about Turing machines are undecidable. A powerful theorem known as Rice’s theorem says that every nontrivial semantic property of a Turing machine is undecidable.
Fix an encoding method and let be the set of all strings that are encoded Turing machines, i.e., For any Turing machine , let
Definitions. A property of Turing machines is a subset . We say that a Turing machine has property if .
is nontrivial if both and its complement in are nonempty sets.
is syntactic if there exist two Turing machines and such that , but only one has property (i.e., the difference between the machines is in the syntax of the algorithm, not the languages they recognize).
is semantic if it is not syntatic. So if two Turing
machines recognize the same language, then either they both have
property
or they both don’t.
Here are some examples of properties. For each example, determine whether it is a syntactic or semantic property.
Rice’s Theorem. Every nontrivial semantic property is undecidable.
We proved Rice’s theorem using a proof by contradiction (see below). Our book also has a different proof in Section 5.3 if you are interested.
Proof. Suppose is a Turing machine with property and is a Turing machine that doesn’t have . We can assume without loss of generality that . Then for any Turing machine and string , construct a new Turing machine that starts by running on until that halts, then it runs on the actual input, returning whatever returns. So Therefore has property if and only if halts on .
Today we introduced big-O notation and used it to talk about running times of algorithms.
Definition (Big-O notation). Let . We say that if there are constants such that for all . So is the set of all functions that are eventually bounded by for some constant .
Note that there are lots of important examples in Barak Chapter 12 of algorithms and their running times.
We proved the following facts about big-O notation:
Theorem (Only Dominant Terms Matter). If is a sum of nonnegative functions , then there is at least one function such that . We call that function a dominant term for .
Theorem (Constants Don’t Matter). For any and constant , and .
Theorem (Products of Functions). If and , then .
We get this hierarchy of functions:
We used these ideas to find the dominant term for these expressions:
.
.
So why do we use big-O notation? It makes it easier to talk about a lot of formulas. For example, an algorithm that requires steps can be described simply as being .
Caution 1. Big-O notation only gives an upper bound for how fast functions grow. Functions in don’t have to grow at the same rate as , they can also grow much slower.
Caution 2. You should always write the simplest possible expression inside big-O notation. For example , so just write .
We finished by talking about how we use big-O notation to describe the runtime of algorithms. Consider the language Here is a simple algorithm to decide :
We started with this example:
Find an algorithm that determines whether a binary number is divisible by 7. Hint: if is a positive integer written in binary and you add a zero at the end, what number do you get? What if you add a 1 at the end. How could you use this idea to keep track of the remainder modulo 7 as you read a binary number?
What is the time complexity of the algorithm above?
It turns out that the language is a regular language. For regular languages, we proved the following result.
Theorem. If is regular, then can be decided in time.
Last time we saw an algorithm that can decide in steps using a simple algorithm. There are actually better algorithms that can decide faster. Here’s one:
You can go even faster with a multi-tape Turing machine.
Theorem (Multi-tape speedup). If , then any multi-tape Turing machine that runs in steps can be simulated by a single-tape Turing machine in steps.
Theorem (Nondeterministic speedup). If , then any nondeterministic Turing machine that runs in steps can be simulated by a deterministic Turing machine in steps, that is, the time complexity is at most for some constant .
We talked about how to prove the second theorem by considering the computation tree for a nondeterministic Turing machine. If the NTM runs in , steps, then a breadth first simulation of the NTM must check an exponential number of branches where is the maximum number of branches at each step. Each branch requires steps to simulate, so the total run time of the deterministic TM is which can be expressed as .
| Day | Section | Topic |
|---|---|---|
| Mon, Apr 7 | 6.2 | The complexity class P |
| Wed, Apr 9 | 6.2 | The complexity class P |
| Fri, Apr 11 | B8.1 | RAM machines |
Today we started by talking about problem #4 on homework 9. We also looked at examples using Rice’s theorem like problem #3. Then we introduced the following class of languages which can be decided in polynomial time.
Definition. A language is in class P (denoted ) if there is a Turing machine and a such that can decide in time.
Today we did this in-class workshop to prove that all context-free languages are in class P.
Today we looked at some examples of languages that are in class P. We also briefly discussed random access memory (RAM) machines which are sometimes a more convenient model for discussing time complexity. It turns out that any problem that can be solved in polynomial time by a RAM machine can also be solved in polynomial time by a Turing machine. There is more in Barak Chapter 8 about RAM machines.
Let . Estimate the time complexity of the following algorithm:
If are both in class , then prove that the concatenation is in class P. Hint: if , then there exist and such that is the concatenation . So to check if , you just need to check if can be decomposed into where and .
Estimate the time complexity of the Euclidean algorithm for finding the greatest common divisor of two positive integers:
def gcd(a, b):
while (b != 0):
t = b
b = a % b
a = t
return aHint: For every two steps of the while loop, the size of will decrease by a factor of at least 2, and will be strictly smaller than .
| Day | Section | Topic |
|---|---|---|
| Mon, Apr 14 | 6.3 | The complexity class NP |
| Wed, Apr 16 | 6.5 | NP-complete languages |
| Fri, Apr 18 | 6.5 | NP-complete languages |
A verifier for a language is a Turing machine such that The string is called the solution or certificate for .
Consider the language COMPOSITE . This language is hard to decide, but it is easy to verify that a number is composite if someone tells you two of its factors. For example .
It turns out that long multiplying two -bit integers can be done in time.
A language is in class NP (also known as polynomial time verifiable) if there is a verifier for that runs in polynomial time as a function of the length of the input string . We don’t make any assumptions about the length of the solution string or how long it will take to find .
We showed that these languages are both in class NP:
COMPOSITE .
3-CLIQUE .
We also proved this theorem:
Theorem. P NP.
Why doesn’t the following algorithm show that COMPOSITE is in class P?
# Input: An integer N > 1
for k = 2 to N-1:
if (N % k == 0):
ACCEPT
# If N has no smaller divisors after the loop, then
REJECTWe also stated and gave a hand-wavy proof of this result:
Theorem. A language is in class NP if and only if there is a nondeterministic Turing Machine that decides in polynomial time.
Along the way, we mentioned some interesting new results:
It is still unknown whether P NP.
Today we introduced the Boolean satisfiability problem (SAT).
Definition. A Boolean function is satisfiable if there is an input such that .
Show that the Boolean function is satisfiable.
Give an example of a Boolean function that is not satisfiable.
A Boolean formula is a string involving variables and the logical operators AND (), OR (), and NOT (denoted by or a line on top of a variable). Consider the following language:
Prove that SAT is decidable.
Prove that SAT is in NP.
It turns out that SAT is actually an NP-complete language, which means that if SAT turns out to be in P, then so does every NP language! That’s a theorem that we aren’t ready to prove yet, but one of the key ideas in the proof is to be able to reduce one problem to another problem in polynomial time.
Definition. In a Boolean formula,
A Boolean formula is in conjunctive normal form (CNF) if it consists of a finite number of clauses all connected together by AND operators.
For example
is in CNF.
In logic, a conjunction is when two or more statements are joined with an AND, and a disjunction is when two or more statements are joined with an OR.
An important special case of the SAT problem is the 3-SAT problem, which only looks at Boolean formulas in CNF where the clauses each involve only 3 literals (possibly including repeated literals). So a 3-CNF formula would be something like:
Instead of using a brute force algorithm to decide 3-SAT, we will take a different approach and prove that solving the 3-SAT problem is not much harder than deciding this language:
In fact, we gave the outline of a proof for the following theorem (although we didn’t formally define “polynomial time reducible” yet).
Theorem. 3-SAT is polynomial time reducible to CLIQUE.
The key to link 3-SAT and CLIQUE is to draw a graph where every vertex corresponds to a literal in one of the clauses, and we draw edges according to the following rules:
Then, if a Boolean formula in 3-CNF has -clauses, then it is satisfiable iff the corresponding graph has a -clique (as the following image illustrates):
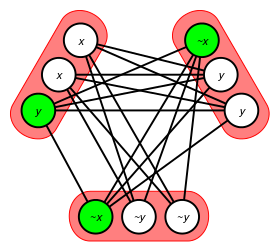
Definition. A language is polynomial time reducible to another language (denoted ) when there is a polynomial time computable function such that for every ,
Last time we proved that we can turn any Boolean formula in 3-conjunctive normal form into a graph , and that the graph has a k-clique (where is the number of clauses in the formula) if and only if the original formula was in 3-SAT.
If our formula has clauses, then how many vertices does the graph have?
What is an upper bound for the number of edges in ?
Based on the previous answers, how long will it take an algorithm to to convert a 3-CNF formula to the graph and number ?
Definition. A language is NP-hard if every in NP is polynomial time reducible to . Languages that are both NP and NP-hard are called NP-complete.
In the early 1970s, researchers in both the USA and Soviet Union were studying algorithms. Cook (USA) and Levin (USSR) gave the first proof that some problems are NP-complete.
Theorem (Cook-Levin). 3-SAT is NP-complete.
There are several proofs of this theorem. They are all a bit technical, but we’ll hopefully take a look at one later. For today we proved the following result.
Then we looked at another example of a polynomial time reduction.
Let
Here is an algorithm to reduce k-SAT to 3-SAT.
It’s not hard to confirm that at every step, the new clauses will be satisfiable if and only if the old clauses were. It is also not hard to verify that this algorithm runs in polynomial time.
| Day | Section | Topic |
|---|---|---|
| Mon, Apr 21 | 6.5 | Examples of NP-complete languages |
| Wed, Apr 23 | Review | |
| Fri, Apr 25 | Midterm 3 | |
| Mon, Apr 28 | TBA |
Today we gave an example of a language that is in NP-complete. For an (undirected) graph we say that a set of vertices is a vertex cover for if every edge in is adjacent to at least one vertex in the cover. Let
Theorem. .
We spent the rest of class explaining the proof. The first part is easier:
The harder part of the theorem is to prove that VERTEX-COVER is NP-hard. The standard way to do this is to show that there is a polynomial time reduction from a problem we already know is NP-hard to VERTEX-COVER.
Claim. .
To prove this claim we had to describe a polynomial time function that converts any Boolean formula in 3-CNF to a graph and an integer such that has a vertex-cover with elements if and only if is satisfiable. Here’s how the graph is constructed.
For each variable , create two blue nodes connected by a blue edge. Label the nodes and respectively.
For each clause, create three red nodes all connected in a triangle with three edges. Label these nodes with the literals from the clause.
Draw a black edge from each red node to the blue node with the same label.
In addition to finding , the constant is set equal to
We did this example:
Draw the graph above for the Boolean formula .
How many passes through a string will it take to construct a string representing ? Can it be done in polynomial time?
Once we determined that this construction can be done in polynomial time, we had to show that
() Suppose is satisfiable. Consider a satisfying assignment of values to the variables of . For every true literal, add the corresponding blue node of to the cover. Notice that one node in each each red triangle must be connected by a black edge to a blue node in the cover. So we can add the other two red nodes from each triangle and cover every red edge and the other black edges.
() Suppose we have a vertex cover for with exactly elements. Every blue edge must have one blue node in the cover. Every red triangle must have at least 2 nodes in the cover to reach every red edge. That uses up all of the nodes in the cover (I got a little confused about this point in class, but the solution is pretty simple!). Set the value of each blue literal in the cover to TRUE. Since each red triangle has one node not in the cover, that node’s black edge must connect to a true literal, so each red clause is true making the whole Boolean formula satisfiable.
Today we went over problems 1 through 3 from homework 11 in detail. Then we also went over problem 8 from the midterm 3 review.
Today we went over this problem from midterm 3:
We started by talking about the brute-force algorithm for deciding if a graph is bipartite, and why it isn’t polynomial time. Then we talked about finding a better algorithm, and verifying that the improved algorithm does run in polynomial time.
We finished by talking about the traveling salesman problem: For a given weighted graph, find the minimum cost path that visits every vertex exactly once and then returns to the start vertex.