Numerical Analysis Notes

Math 342 - Spring 2026

Week 1 Notes

Mon, Jan 12

We talked about how computers store floating point numbers. Most modern programming languages store floating point numbers using the IEEE 754 standard.

In the IEEE 754 standard, a 64-bit floating point number has the form

$$\mathbf{value} = (-1)^\mathbf{sign} \, \times \, 2^{(\mathbf{exponent} - 1023)} \, \times \, (1 + \mathbf{fraction})$$

where

• $\mathbf{sign}$ is a single bit: 0 for positive, 1 for negative.
• $\mathbf{fraction}$ is a 52-bit fraction (in binary) with $0 \le \mathbf{fraction} < 1$.
• $\mathbf{exponent}$ is the 11-bit binary integer which ranges from 0 to 2047. Only 1 to 2046 are used for regular floating point numbers, $\mathbf{exponent}=0$ is reserved for zero and subnormal numbers, and $\mathbf{exponent}=2047$ is reserved for infinity and NaN (“not a number”).

We talked about how to convert between binary numbers and decimal numbers. This system works very well, but it leads to weird outcomes like 0.1 + 0.1 + 0.1 = 0.30000000000000004.

When you convert $\tfrac{1}{10} = 0.1$ to binary, you get a infinitely repeating binary decimal: $$\tfrac{1}{10} = (0.000110011001100\ldots)_2.$$ So any finite binary representation of $\tfrac{1}{10}$ will have rounding errors.

We did the following examples in class:

1. Convert (10110)₂ to decimal. (https://youtu.be/a2FpnU9Mm3E)

2. Convert 35 to binary. (https://youtu.be/gGiEu7QTi68)

3. What is the 64-bit string that represents the number 35 in the IEEE standard?

4. What are the largest and smallest 64-bit floating point numbers that can be stored?

5. In Python, compute 2.0**1024 and 2**1024. Why do you get different results?

6. In Python, compare 2.0**1024 with 2.0**(-1024) and 2.0**(-1070). What do you notice?

Wed, Jan 14

Today we talked about significant digits. Here is a quick video on how these work.

Next we defined absolute and relative error:

The base-10 logarithm of the relative error is approximately the number of significant digits, so you can think of significant digits as a measure of relative error.

Intuitively, addition & subtraction “play nice” with absolute error while multiplication and division “play nice” with relative error. This can lead to problems:

1. Catastrophic cancellation. When you subtract two numbers of roughly the same size, the relative error can get much worse. For example, both 53.76 and 53.74 have 4 significant digits, but $$53.76 - 53.74 = 0.02$$ only has 1 significant digit.

2. Useless precision. If you add two numbers with very different magnitudes, then having a very low relative error in the smaller one will not be useful.

We did these examples in class.

1. $\pi = 3.141592...$. What is the absolute and relative error if your round $\pi$ to $3.14$?

You can sometimes re-write algorithms on a computer to avoid issues with floating point numbers such as overflow/underflow and catastrophic cancellation.

2. Consider the function $f(x) = \dfrac{1 - \cos x}{\sin x}$. Use Python to compute $f(10^{-7})$.

3. The exact answer to previous question is $0.00000005 = 5 \times 10^{-8}$ (accurate to 22 decimal places). Use this to find the relative error in your previous calculation.

4. A better way to compute $f(x)$ is to use a trick to avoid the catastrophic cancellation: $$f(x) = \dfrac{1-\cos x}{\sin x} = \dfrac{1 - \cos x}{\sin x} \cdot \left( \frac{1+ \cos x}{1+\cos x} \right) = \dfrac{\sin x}{1 + \cos x}.$$ Use this new formula to compute $f(10^{-7})$. What is the relative error now?

Stirling’s formula is a famous approximation for the factorial function. $$n! \approx \sqrt{2 \pi n} \frac{n^n}{e^n}.$$ We approximated Stirling’s formula using the following code.

import math
n = 100
print(float(math.factorial(n)))
f = lambda n: math.sqrt(2 * math.pi * n) * n ** n / math.exp(n)
print(f(n))

Our formula worked well until $n=143$, then we got an overflow error. The problem was that $n^n$ got too big to convert to a floating point number. But you can prevent the overflow error by adjusting the formula slightly to.

n = 143
f = lambda n: math.sqrt(2 * math.pi * n) * (n / math.e) ** n
print(f(n))

Fri, Jan 26

Today we reviewed Taylor series. We recalled the following important Maclaurin series (which are Taylor series with center $c = 0$):

• $e^x = \sum_{n=0}^\infty \dfrac{x^n}{n!}$
• $\sin(x) = \sum_{n=0}^\infty \dfrac{(-1)^n \, x^{2n+1}}{(2n+1)!}$
• $\cos(x) = \sum_{n=0}^\infty \dfrac{(-1)^n \, x^{2n}}{(2n)!}$
• $\dfrac{1}{1-x} = \sum_{n = 0}^\infty x^n$
• $\ln(1+x) = \sum_{n = 0}^\infty \dfrac{(-1)^n \, x^{n+1}}{n+1}$

We graphed Maclaurin polynomials for $\cos x$ and $\dfrac{1}{1-x}$ on Desmos to see how they converge with different radii of convergence.

We also use the Maclaurin series for $\dfrac{\sin x}{x}$ to approximate the integral

$$\displaystyle \int_{-\pi}^\pi \frac{\sin x}{x} \, dx.$$

Then we did the following workshop in class.

• Workshop: Taylor series

Week 2 Notes

Wed, Jan 21

Today we reviewed some theorems that we will need throughout the course. The first is probably the most important theorem in numerical analysis since it lets us estimate error when using Taylor series approximations.

A special case of Taylor’s theorem is when $n = 0$. Then you get the Mean Value Theorem (MVT):

We did this example:

1. Use Taylor’s theorem to estimate the error in using the 0th and 2nd degree Maclaurin polynomials to estimate $\cos(0.03)$ and $\cos(0.6)$.

Then we started this workshop

• Workshop: Error bounds

Fri, Jan 23

Last time we started this workshop about using Taylor’s remainder formula and the triangle inequality to find upper bounds for functions. Today we revisited that workshop, but first we talked about the following.

This error formula gives a way to estimate the worst case (absolute) error when you use a Taylor polynomial approximation.

1. The 3rd degree Taylor polynomial for $\cos x$ centered at $c = \pi$ is $P_3(x) = -1 + \tfrac{1}{2}(x-\pi)^2$ (the coefficient on the 3rd degree term is zero). What is the worst case absolute error using this polynomial to estimate $\cos 3$?

After that we talked about the triangle inequality.

We talked about how you can use the triangle inequality to find upper bounds for functions. We also talked about tight upper bounds versus upper bounds that are not tight. We did this example.

2. Use the triangle inequality to find an upper bound for $|x^2 + 3x \cos x|$.

Week 3 Notes

Wed, Jan 28

We talked about how to find the roots of a function. Recall that a root (AKA a zero) of a function $f(x)$ is an $x$-value where the function hits the $x$-axis. We introduced an algorithm called the bisection method for finding roots of a continuous function that changes sign from positive to negative or negative to positive on an interval $[a, b]$. We wrote the following code to implement this algorithm.

def bisection(f, a, b, N):
    """
    Applies the bisection method recursively up to N times to estimate a root 
    of a continuous function f on an interval [a,b]. 
    """
    m = (a + b) / 2
    if N == 0 or f(m) == 0:
        return m
    if (f(a) > 0 and f(m) > 0) or (f(a) < 0 and f(m) < 0):
        return bisection(f, m, b, N - 1)
    else:
        return bisection(f, a, m, N - 1)

We tested this algorithm on the function $f(x) = \tan x - 1$ which has a root at $\tfrac{\pi}{4}$.

One feature of the bisection method is that we can easily find the worst case absolute error in our approximation of a root. That is because every time we repeat the algorithm and cut the interval in half, the error reduces by a factor of 2, so that $$\text{Absolute error} \le \frac{(b-a)}{2^{N+1}}.$$ We saw that it takes about 10 iterations to increase the accuracy by 3 decimal places (because $2^{10} \approx 10^3$).

Fri, Jan 30

Today we covered Newton’s method. This is probably the most important method for finding roots of differentiable functions. The formula is $$x_{n+1} = x_n - \dfrac{f(x_n)}{f'(x_n)}.$$ This formula comes from the idea which is to start with a guess $x_0$ for a root and then repeatedly improve your guess by following the tangent line at $x_n$ until it hits the $x$-axis.

1. Use Newton’s method to find roots of $\tan x - 1$.

2. How can you use Newton’s method to find $e$? Hint: use $f(x) = \ln x -1$.

Proof. Start with the first degree Taylor polynomial (centered at $x_n$) for $f(r)$ including the remainder term and the Newton’s method iteration formula:

$$f(r) = f(x_n) + f'(x_n)(r-x_n) + \frac{1}{2} f''(z)(r-x_n)^2 = 0,$$ and $$x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} \Rightarrow f'(x_n)(x_{n+1} - x_n) + f(x_n)=0.$$

Subtract these two formulas to get a formula that relates $(r-x_{n+1})$ with $(r-x_n)$.

$$f'(x_n)(r-x_{n+1}) + \frac{1}{2} f''(z)(r-x_n)^2 = 0.$$

Use this to get an upper bound on $|r-x_{n+1}|$. □

This corollary explains why, if you start with a good guess in Newton’s method, the number of correct decimal places tends to double with each iteration!

Week 4 Notes

Mon, Feb 2

The secant method is a variation of Newton’s method that uses secant lines instead of tangent lines. The advantage of the secant method is that it doesn’t require calculating a derivative. The disadvantage is that it is a little slower to converge than Newton’s method, but it is still much faster than the bisection method. Here is the formula:

$$x_{n+1} = x_n - \frac{f(x_n) \, (x_n - x_{n-1})}{f(x_n) - f(x_{n-1})}.$$

1. Solve the equation $2^x = 10$ using the secant method. What would make good initial guesses $x_0$ and $x_1$?

    # This code will do one step of the secant method.
    f = lambda x: 2 ** x - 10
    a, b = 3, 3.5
    a, b = b, b - f(b) * (b - a) / (f(b) - f(a)); print(b)

Convergence of order $\alpha = 1$ is called linear convergence and convergence of order $\alpha = 2$ is called quadratic convergence. Newton’s method converges quadratically. It turns out that the secant method converges with order $\alpha = \frac{1+\sqrt{5}}{2} \approx 1.618$ which is the golden ratio!

• Workshop: Root finding methods

Wed, Feb 4

Newton’s method is a special case of a method known as fixed point iteration. A fixed point of a function $f(x)$ is a number $p$ such that $f(p) = p$. A real-valued function $f(x)$ has a fixed point on an interval $[a, b]$ if and only if it intersects the graph $y = x$ on that interval.

1. Show that $\cos x$ has a fixed point in $[0,\tfrac{\pi}{2}]$.

2. Explain why $f(x) = e^x$ has no fixed points.

3. Does $\sin x$ have any fixed points?

A fixed point $p$ is attracting if the recursive sequence defined by $x_{n+1} = f(x_n)$ converges to $p$ for all $x_0$ sufficiently close to $p$. It is repelling if points close to $p$ get pushed away from $p$ when you apply the function $f$. You can draw a picture of these fixed point iterates by drawing a cobweb diagram.

To make a cobweb diagram, repeat these steps:

• Move vertically from your current x-value until you hit the graph $y = f(x)$.
• Now move horizontally to the graph $y = x$.

4. Show that the fixed point of $\cos x$ is attracting by repeatedly iterating.

5. Show that $g(x) = 1 - 2x -x^5$ has a fixed point, but it is not attracting.

Proof. Write down the first degree Taylor approximation for $f$ centered at $p$. Use it with $x = x_n$, $f(x_n) = x_{n+1}$ to show that if $M$ is an upper bound for $f''(z)$ (near $p$), then $$|x_{n+1} - p| \le |x_n - p| \left(|f'(p)| + \frac{M}{2}|x_n-p| \right).$$ Then as long as $x_n$ is close enough to $p$, the terms inside the parentheses are less than 1 which means that $|x_{n+1} - p| < |x_n - p|$, i.e, $x_{n+1}$ is closer to $p$ than $x_n$ for every $n$. □

5. For any function $f \in C^2[a,b]$ with a root $r$ in $(a,b)$, let $g(x) = x - \dfrac{f(x)}{f'(x)}$. Show that $r$ is a fixed point of $g$ and show that $g'(r) = 0$.

Fri, Feb 6

In any root finding method, we have two ways of measuring the error when we compare an approximation $x_n$ with the actual root. The forward error is the distance between the root $r$ and the approximation $x_n$ on the $x$-axis. Since we usually don’t know the true value of $r$, it is hard to estimate the forward error. The backward error is just $|f(x_n)|$, which is usually easy to calculate.

1. If $x_n$ is really close to $r$, then how could you use $f'(r)$ to estimate the forward error if you know the backward error?

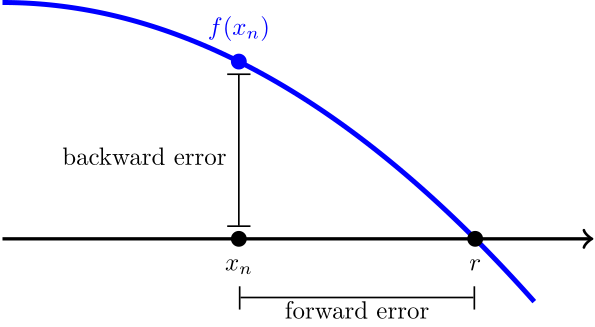
We used the idea of forward and backward error to automate Newton’s method. The idea is to include an optional tolerance argument. We stop iterating when the backward error is smaller than the tolerance.

def newton(f, Df, x, tolerance = 10 ** (-15)):
    """
    Applies Newton's method to a function f with derivative Df and initial guess x.  
    Stops when |f(x)| < tol. 
    """
    step = 0
    while not abs(f(x)) < tolerance:
        x = x - f(x) / Df(x)
        step = step + 1
    print("Converged in", step, "steps.")
    return x

We finished with a cool fact about Newton’s method. It also works for to find complex number roots if you use complex numbers. We did a quick review of complex numbers.

We used the cmath library in Python to do the following experiments with Newton’s method.

2. Cube roots of unity. Use Newton’s method to find all 3 roots of $x^3 - 1$.

3. Euler’s identity. Use Newton’s method to solve $e^x + 1 = 0$.

We finished by talking about Newton fractals. When you use Newton’s method on a function with more than one root in the complex plane, the set of points that converge to each root (called the basins of attraction) form fractal patterns.

Week 5 Notes

Mon, Feb 9

Today we talked about how to solve systems of nonlinear equations with Newton’s method. As a motivating example, we talked about how this could be used in navigation, for example in the LORAN system.

To solve a vector-valued system $\mathbf{F}(\mathbf{x}) = \mathbf{0}$, you can iterate the formula $$\mathbf{x}_{n+1} = \mathbf{x}_n - \mathbf{J}(\mathbf{x}_n)^{-1} \mathbf{F}(\mathbf{x_n})$$ where $\mathbf{J}(\mathbf{x})$ is the Jacobian matrix $$\mathbf{J}(\mathbf{x}) = \begin{bmatrix} \frac{\partial F_1}{\partial x_1} & \ldots & \frac{\partial F_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial F_n}{\partial x_1} & \ldots & \frac{\partial F_n}{\partial x_n} \end{bmatrix}.$$

To program this formula in Python, we’ll need to load the numpy library. We wrote the following code to solve this system:

$$\begin{align*} xy + y^2 &= 1 \\ x^2 - y^2 &= 1 \end{align*}$$

import numpy as np

F = lambda x: np.array([
    x[0] * x[1] + x[1]**2 - 1, 
    x[0]**2 - x[1]**2 - 1
])
J = lambda x: np.array([
    [   x[1], x[0] + 2*x[1] ], 
    [ 2*x[0],       -2*x[1] ]
])

x = np.array([1,1])
for i in range(10): 
    x = x - np.linalg.inv(J(x)) @ F(x) # Use @ not * for matrix multiplication.
    print(x)

• Workshop: Nonlinear systems

Wed, Feb 11

Today we talked about systems of linear equations and linear algebra.

1. Suppose you have a jar full of pennies, nickles, dimes, and quarters. There are 80 coins in the jar, and the total value of the coins is $10.00. If there are twice as many dimes as quarters, then how many of each type of coin are in the jar?

We can represent this question as a system of linear equations. $$p+n+d+q = 80$$ $$p+5n+10d+25q = 1000$$ $$d = 2q$$ where $p,n,d,q$ are the numbers of pennies, nickles, dimes, and quarters respectively. It is convenient to use matrices to simplify these equations: $$\begin{pmatrix} 1 & 1 & 1 & 1 \\ 1 & 5 & 10 & 25 \\ 0 & 0 & 1 & -2 \end{pmatrix} \, \begin{pmatrix} p \\ n \\ d \\ q \end{pmatrix} = \begin{pmatrix} 80 \\ 1000 \\ 0 \end{pmatrix}.$$ Here we have a matrix equation of the form $A\mathbf{x} = \mathbf{b}$ where $A \in \mathbb{R}^{3 \times 4}$, $\mathbf{x} \in \mathbb{R}^4$ is the unknown vector, and $\mathbf{b} \in \mathbb{R}^3$. Then you can solve the problem by row-reducing the augmented matrix

$$\left( \begin{array}{cccc|c} 1 & 1 & 1 & 1 & 80 \\ 1 & 5 & 10 & 25 & 1000 \\ 0 & 0 & 1 & -2 & 0\end{array}\right)$$

which can be put into echelon form

$$\left( \begin{array}{cccc|c} 1 & 1 & 1 & 1 & 80 \\ 0 & 4 & 9 & 24 & 920 \\ 0 & 0 & 1 & -2 & 0\end{array}\right).$$

The variables $p, n$, and $d$ are pivot variables, and the last variable $q$ is a free variable. Once you pick values for the free variable(s), you can solve for the pivot variables one at a time using back substitution. We did this using Python:

q = 20 
d = 2*q
n = (920 - 9*d - 24*q) / 4
p = 80 - n - d - q
print(p, n, q)

# Only q = 20 makes sense, otherwise either p or n will be negative.

After that we reviewed some more concepts and terminology from linear algebra. The most important thing to understand is that you can think of matrix-vector multiplication as a linear combination of the columns of the matrix:

$$A \mathbf{x} = \begin{pmatrix} 1 & 1 & 1 & 1 \\ 1 & 5 & 10 & 25 \\ 0 & 0 & 1 & -2 \end{pmatrix} \, \begin{pmatrix} p \\ n \\ d \\ q \end{pmatrix} = \underbrace{\begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}p + \begin{pmatrix} 1 \\ 5 \\ 0 \end{pmatrix}n + \begin{pmatrix} 1 \\ 10 \\ 1 \end{pmatrix}d + \begin{pmatrix} 1 \\ 25 \\ -2 \end{pmatrix}q}_{A \mathbf{x} \text{ is a linear combination of the columns of } A}.$$

For any matrix $A \in \mathbb{R}^{m \times n}$:

• The column space of $A$ is the set of all possible linear combinations of the columns. It is also the range of $A$ as a linear transformation from $\mathbb{R}^n$ into $\mathbb{R}^m$.

• The rank of $A$ is the dimension of the column space. It is also the number of pivots, since the pivot columns are a basis for the column space.

• The null space of $A$ is the set $\{\mathbf{x} \in \mathbb{R}^n \, : \, A \mathbf{x} = \mathbf{0}\}$.

• The nullity of $A$ is the number of free variables which is the same as the dimension of the null space of $A$.

A matrix equation $A\mathbf{x} = \mathbf{b}$ has a solution if and only if $\mathbf{b}$ is in the column space of $A$. If $\mathbf{b}$ is in the column space, then there will be either one unique solution if there are no free variables (i.e., the nullity of $A$ is zero) or there will be infinitely many solutions if there are free variables.

If $A \in \mathbb{R}^{n \times n}$ (i.e., $A$ is a square matrix) and the rank of $A$ is $n$, then $A$ is invertible which means that there is a matrix $A^{-1}$ such that $A A^{-1} = A^{-1} A = I$ where $I$ is the identity matrix which is $$I = \begin{pmatrix} 1 & 0 & \ldots & 0 \\ 0 & 1 & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & 1 \end{pmatrix}.$$
You can use row-reduction to find the inverse of an invertible matrix by row reducing the augmented matrix $\left[ \begin{array}{c|c} A & I \end{array} \right]$ until you get $\left[ \begin{array}{c|c} I & A^{-1} \end{array} \right]$. We did this example in class:

2. Find the inverse of $A = \begin{pmatrix} 1 & 2 & 0 \\ 0 & 1 & 3 \\ 0 & 0 & 1 \end{pmatrix}$.

Here is another example that we did not do in class:

3. Use row-reduction to find the inverse of $A = \begin{pmatrix} 1 & 3 \\ 2 & 5 \end{pmatrix}$. (https://youtu.be/cJg2AuSFdjw)

Fri, Feb 13

Today we talked about LU decomposition. We defined the LU decomposition as follows. The LU decomposition of a matrix $A \in \mathbb{R}^{m \times n}$ is a pair of matrices $L \in \mathbb{R}^{m \times m}$ and $U \in \mathbb{R}^{m \times n}$ such that $A = LU$ and $U$ is in echelon form and $L$ is a lower triangular matrix with 1’s on the main diagonal, 0’s above the main diagonal, and entries $L_{ij}$ in row $i$, column $j$ that are equal to the multiple of row $i$ that you subtracted from row $j$ as you row reduced $A$ to $U$.

1. Compute the LU decomposition of $A = \begin{pmatrix} 1 & 1 & 1 & 1 \\ 2 & 2 & 5 & 3 \\ -1 & -1 & 14 & 4 \end{pmatrix}$.

2. Use the LU decomposition to solve $Ax = \begin{pmatrix} 2 \\ 6 \\ 8 \end{pmatrix}$.

We also did this workshop.

• Workshop: LU decomposition

We finished with one more example.

3. For what real numbers $a$ and $b$ does the matrix $\begin{pmatrix} 1 & 0 & 1 \\ a & a & a \\ b & b & a \end{pmatrix}$ have an LU decomposition? (https://youtu.be/-eA2D_rIcNA)

Here’s another LU decomposition example if you want more practice.

4. Decompose $A = \begin{pmatrix} 2 & 4 & 3 & 5 \\ -4 & -7 & -5 & -8 \\ 6 & 8 & 2 & 9 \\ 4 & 9 & -2 & 14 \end{pmatrix}$. (https://youtu.be/BFYFkn-eOQk)

Week 6 Notes

Mon, Feb 16

1. Let $A = \begin{pmatrix} 1 & 1 \\ 1 & 1.001 \end{pmatrix}$. Let $\mathbf{y} = \begin{pmatrix} 2 \\ 2 \end{pmatrix}$ and $\mathbf{z} = \begin{pmatrix} 2 \\ 2.001 \end{pmatrix}$. Use $A^{-1} = \begin{pmatrix} 1001 & -1000 \\ -1000 & 1000 \end{pmatrix}$ to solve $A\mathbf{x} = \mathbf{y}$ and $A\mathbf{x} = \mathbf{z}$.

Notice that even though $\mathbf{y}$ and $\mathbf{z}$ are very close, the two solutions are not close at all. When the solutions of a linear system $A\mathbf{x} = \mathbf{b}$ are very sensitive to small changes in $b$, we say that the matrix $A$ is ill-conditioned.

Norms of Vectors

Intuitively a norm measures the length of a vector. But there are different norms and they measure length in different ways. The three most important norms on the vector space $\mathbb{R}^n$ are:

1. The $2$-norm (also known as the Euclidean norm) is the most commonly used, and it is exactly the formula for the length of a vector using the Pythagorean theorem. $$\|x\|_2 = \sqrt{x_1^2 + x_2^2 + \ldots + x_n^2}.$$

2. The $1$-norm (also known as the Manhattan norm) is $$\|x\|_1 = |x_1|+|x_2|+\ldots+|x_n|.$$ This is the distance you would get if you had to navigate a city where the streets are arranged in a rectangular grid and you can’t take diagonal paths.

3. The $\infty$-norm (also known as the Maximum norm) is $$\|x\|_\infty = \max \{ |x_1|, |x_2|, \ldots, |x_n| \}.$$

These are all special cases of $p$-norms which have the form $$\|x\|_p = \sqrt[p]{|x_1|^p + |x_2|^p + \ldots + |x_n|^p}.$$

We used Desmos to graph the set of vectors in $\mathbb{R}^2$ with $p$-norm equal to one, then we could see how those norms change as $p$ varies between 1 and $\infty$.

Norms of Matrices

The set of all matrices in $\mathbb{R}^{m \times n}$ is a vector space. So it makes sense to talk about the norm of a matrix. There are many ways to define norms for matrices, but the most important for us are the induced norms (also known as operator norms). For a matrix $A \in \mathbb{R}^{m \times n}$, the induced $p$-norm is $$\|A\|_p = \max \{\|Ax\|_p : x \in \mathbb{R}^n, \|x\|=1\}.$$
Two important special cases are

1. When $p=2$, the induced norm $\|A\|_2$ is the square root of the largest eigenvalue of $A^T A$.
   
2. When $p=\infty$, the induced norm $\|A\|_\infty$ is the largest 1-norm of the rows of $A$.

Here is a quick exercise:

2. Find $\|A\|_\infty$ for the matrix $A = \begin{pmatrix} 1 & 1 & 1 & 1 \\ 2 & 2 & 5 & 3 \\ -1 & -1 & 14 & 4 \end{pmatrix}$.

Condition Number

For an invertible matrix $A \in \mathbb{R}^{n \times n}$, the condition number of $A$ is $\kappa(A) = \|A\| \, \|A^{-1}\|$. You can use any induced norm to define $\kappa(A)$, but our default will be the induced $\infty$-norm since it is the only one that is easy to calculate by hand.

3. Find the condition number $\kappa(A)$ for the matrix $A = \begin{pmatrix} 1 & 1 \\ 1 & 1.001 \end{pmatrix}$ with $A^{-1} = \begin{pmatrix} 1001 & -1000 \\ -1000 & 1000 \end{pmatrix}$.

If the condition number is large, then the matrix is ill-conditioned. When we try to solve an ill-conditioned linear system, small errors in either $A$ or $\mathbf{b}$ could become large errors in our calculated solution.

Just like with root finding, we can talk about forward and backward error when we try to solve a linear system $A \mathbf{x} = \mathbf{b}$. The table below defines the absolute and relative forward and backwards errors. In the table, $\mathbf{x}$ is the exact solution to the system $A \mathbf{x} = \mathbf{b}$, and $\mathbf{x}_a$ is an approximation of $\mathbf{x}$.

The following result shows how the condition number lets us estimate the relative forward error using the relative backward error.

Proof. By the definition of the induced norm, $$\dfrac{\|\mathbf{x}_a - \mathbf{x}\|}{\|\mathbf{x}\|} = \dfrac{\|A^{-1} (A\mathbf{x}_a - \mathbf{b}) \|}{\|\mathbf{x}\|} \le \|A^{-1}\| \dfrac{\|A \mathbf{x}_a - \mathbf{b} \|}{\|\mathbf{x}\|}.$$ Since $\mathbf{b} = A \mathbf{x}$, $\|\mathbf{b}\| \le \|A \| \|\mathbf{x}\|$, so $$\|A^{-1}\| \dfrac{\|A \mathbf{x}_a - \mathbf{b} \|}{\|\mathbf{x}\|} \le \|A^{-1}\| \|A\| \dfrac{\|A \mathbf{x}_a - \mathbf{b} \|}{\|\mathbf{b}\|} = \kappa(A) \dfrac{\|A \mathbf{x}_a - \mathbf{b} \|}{\|\mathbf{b}\|}$$ which proves the statement. □

The following is a consequence of this theorem.

Rule of thumb. If the entries of $A$ and $\mathbf{b}$ are both accurate to $n$-significant digits and the condition number of $A$ is $\kappa(A) = 10^k$, then the solution of the linear system $A\mathbf{x} = \mathbf{b}$ will be accurate to $n-k$ significant digits.

Week 7 Notes

Mon, Feb 23

Consider the matrix $B = \begin{pmatrix} 0.001 & 1 \\ 1 & 1 \end{pmatrix}$ which has $LU$ decomposition $$B = LU = \begin{pmatrix} 1 & 0 \\ 1000 & 1 \end{pmatrix} \, \begin{pmatrix} 0.001 & 1 \\ 0 & -999 \end{pmatrix}.$$
Although $B$ is not ill-conditioned, you have to be careful using row reduction to solve equations with this matrix because both $L$ and $U$ in the LU-decomposition for $B$ are ill-conditioned.

In Matlab/Octave, you can use the norm(A, inf) function to find the induced $\infty$-norm of matrix. The function norm(A) computes the induced 2-norm by default. You can also compute the condition number of a matrix using cond(A) or cond(A, inf).

1. Use Octave to find the condition numbers for the matrices $B$, $L$, and $U$ above.

    B  = [0.001 1; 1 1]
    L = [1 0; 1000 1]
    U = [0.001 1; 0 -999]
    cond(B)
    cond(L)
    cond(U)

It is possible to avoid this problem using the method of partial pivoting. The idea is that there is a permutation $P$ such that $$PA = LU$$ where $P$ is a permutation matrix such that $PA$ has a nice LU-decomposition. The formula $PA = LU$ is known as the PLU-decomposition or sometimes the LUP-decomposition of $A$. This method fixes two problems:

• When there are zero entries where pivots should be, you can’t do a regular LU-decomposition.
• When you do an LU-decomposition, the matrices L and U might be ill-conditioned, even if $A$ isn’t. The method of partial pivots avoids that problem.

The algorithm to find the PLU-decomposition is almost the same as the LU decomposition, except you also swap rows so that the largest available entry in a column (in absolute value) becomes the pivot at each step. When you swap two rows of the echelon form matrix $U$, you also have to swap the same rows of $A$ and the same rows in the completed columns of $L$ (leave the unfinished columns alone). The permutation matrix $P$ is the matrix you get by swapping the same rows of the identity matrix as you swapped while you found the PLU decomposition.

In Octave, you can just use the following command to get the PLU-decomposition:

[L, U, P] = lu(A)

One nice thing to know about permutation matrices is that they are always invertible and $P^{-1} = P^T$ where $P^T$ is the transpose of $P$ obtained by converting every row of $P$ to a column of $P^T$.

2. Show that when you use partial pivoting to row reduce $B = \begin{pmatrix} 0.001 & 1 \\ 1 & 1 \end{pmatrix}$ to echelon form, the resulting LU matrices are not ill-conditioned.

3. Use the PLU-decomposition to solve $B\mathbf{x} = \begin{pmatrix} 1 \\ 2 \end{pmatrix}.$

Finding the PLU decomposition by hand is tedious, especially if you need to swap more than 2 rows, but here is a good video explanation of how it works:

4. Find the PLU decomposition for $A = \begin{pmatrix} 0 & 1 & 2 & 1 & 2 \\ 1 & 0 & 0 & 0 & 1 \\ 2 & 1 & 2 & 1 & 5 \\ 1 & 2 & 4 & 3 & 6 \end{pmatrix}$. (https://youtu.be/E3cCRcdFGmE)

Wed, Feb 25

The inner product of two vectors $\mathbf{x}, \mathbf{y}$ in $\mathbb{R}^n$ is $\mathbf{x}^T \mathbf{y}$. We proved some important facts about inner products and got some practice with matrix algebra in the following workshop:

• Workshop: Inner products & orthogonality

Fri, Feb 27

In exercise 2 from the workshop last time, we needed the property that $(\mathbf{x} + \mathbf{y})^T = \mathbf{x}^T + \mathbf{y}^T$. This is a special case of one of the rules for transposes:

• $(A + B)^T = A^T + B^T$.
  
• $(AB)^T = B^T A^T.$

Today we talked about two special types of matrices.

• A symmetric matrix is a matrix in $\mathbb{R}^{n \times n}$ such that $A^T = A$.
• An orthogonal matrix is a matrix in $\mathbb{R}^{n \times n}$ such that $A^T A = I$.

A set of vectors $S = \{\mathbf{v}_1, \ldots, \mathbf{v}_d\}$ is an orthogonal set if every vector in $S$ is orthogonal to every other vector in $S$. An orthogonal set where every vector also has length equal to 1 is called an orthonormal set.

1. Suppose that we have an orthonormal set in $\mathbb{R}^2$ that contains two vectors $\mathbf{x}$ and $\mathbf{y}$. If $\mathbf{x} = \begin{pmatrix} \cos \theta \\ \sin \theta \end{pmatrix}$ for some angle $\theta$, then there are only two possible vectors that $\mathbf{y}$ could be. What are they? Hint: Draw a picture!

2. If a matrix $U$ in $\mathbb{R}^{m \times n}$ has orthonormal columns, then $U^T U$ is the n-by-n identity matrix. Use this fact to prove that $U$ preserves inner-products. That is $$(U\mathbf{x})^T (U \mathbf{y}) = \mathbf{x}^T \mathbf{y}$$ for any vectors $\mathbf{x}, \mathbf{y}$ in $\mathbb{R}^n$.

3. If $U$ has orthonormal columns, then show that $U$ preserves lengths, that is, $\|U\mathbf{x}\| = \|\mathbf{x}\|$ for all $\mathbf{x}$ in $\mathbb{R}^n$.

A square matrix with orthonormal columns is called an orthogonal matrix.

4. Show that every 2-by-2 orthogonal matrix must be either $$\begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{pmatrix} \text{ or } \begin{pmatrix} \cos \theta & \sin \theta \\ \sin \theta & -\cos \theta \end{pmatrix}.$$

The first possibility represents all possible rotations of $\mathbb{R}^2$. The second represents all possible reflections. Those are the only length-preserving linear transformations of the plane!

We finished by talking about symmetric matrices. A matrix $A$ in $\mathbb{R}^{n \times n}$ is symmetric if $A^T = A$.

5. Suppose that $\mathbf{x}$ and $\mathbf{y}$ are eigenvectors of a symmetric matrix $A$ that correspond to two different eigenvalues $\lambda$ and $\mu$ respectively. Prove that $\mathbf{x}$ is orthogonal to $\mathbf{y}$.
   Hint: Observe that $(A\mathbf{x})^T \mathbf{y} = \mathbf{x}^T (A\mathbf{y})$.

It turns out that symmetric matrices can only have real eigenvalues and they always have an orthonormal basis of eigenvectors.

Since we had a little extra time, we finished by talking about the conjugate transpose of a complex matrix. For any matrix $A$ in $\mathbb{C}^{m \times n}$, the conjugate transpose is $A^* = (\bar{A})^T$. It combines taking the transpose of $A$ with computing the complex conjugate of every entry. Recall that the complex conjugate of a complex number $\overline{a+ib} = a - ib$. For matrices with real number entries, $A^*$ and $A^T$ are the same thing. In Matlab/Octave you use an apostrophe to get the conjugate transpose:

A = [1 2i; 3 4i]
A'

The conjugate transpose mostly has the same properties as the transpose:

• $(A + B)^* = A^* + B^*$
• $(AB)^* = B^* A^*$

One very important exception is when you work with inner-products of complex vectors. The complex inner-product of $\mathbf{x}, \mathbf{y}$ in $\mathbb{C}^n$ is $\mathbf{x}^* \mathbf{y}$. But unlike regular inner-products, order matters for complex inner-products because $$\mathbf{y}^* \mathbf{x} = \overline{\mathbf{x}^* \mathbf{y}}.$$

Week 8 Notes

Mon, Mar 2

Last week we introduced the orthogonal complement $W^\perp$ of a set $W$ in $\mathbb{R}^n$. You should know that:

• $W^\perp$ is a subspace of $\mathbb{R}^n$.
• $(W^\perp)^\perp = \operatorname{span} W$.
• If $V$ is a subspace of $\mathbb{R}^n$, then $V$ and $V^\perp$ are called complementary subspaces and $$\operatorname{dim}V + \operatorname{dim}V^\perp = n.$$

1. We looked at the problem of finding $\left\{ \begin{pmatrix} 1 \\ 1\\ 1 \end{pmatrix} \right\}^\perp$ in the context of the fundamental theorem of linear algebra. The orthogonal complement is the nullspace of the matrix $\begin{pmatrix} 1 & 1 & 1 \end{pmatrix}$.
   1. What is the dimension of the nullspace?
   2. What is a basis for the null space?

After that we talked about why orthogonal bases are better. We used this example:

Since the two components of the force of gravity are orthogonal, it is easy find the right coefficients for the force of gravity in the angled basis.

1. Apply Gram-Schmidt to $\mathbf{x}_1 = \begin{pmatrix} 3 \\ 6 \\ 0 \end{pmatrix}$, $\mathbf{x}_2 = \begin{pmatrix} 1 \\ 2 \\ 2 \end{pmatrix}.$ (https://youtu.be/Rz3O6hJ9xZQ)

2. Apply Gram-Schmidt to $\mathbf{x}_1 = \begin{pmatrix} 1\\ 1\\ 1\\ 1\end{pmatrix}$, $\mathbf{x}_2 = \begin{pmatrix} 0\\ 1\\ 1\\ 1\end{pmatrix}$, $\mathbf{x}_3 = \begin{pmatrix} 0\\ 0\\ 1\\ 1\end{pmatrix}$. (https://youtu.be/Rz3O6hJ9xZQ?t=350)

• Example: Desmos graph of the first example.

Wed, Mar 4

We started with these two warm-up problems.

1. Find the orthogonal projection of $\mathbf{y} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}$ onto the line spanned by $\mathbf{x} = \begin{pmatrix} 1 \\ 0 \\ -1 \end{pmatrix}$. Then find two orthogonal vectors $\mathbf{a}$ and $\mathbf{b}$ such that $\mathbf{a}$ lies in the span of $\mathbf{x}$ and $\mathbf{a} + \mathbf{b} = \mathbf{y}$.

2. Find the orthogonal projection of $\mathbf{z} = \begin{pmatrix} 6 \\ -3 \\ 0 \end{pmatrix}$ onto the plane spanned by $\mathbf{x}$ and $\mathbf{y}$.

In order to calculate the second orthogonal projection, we used the following formula:

Notice that this formula is even simpler if the basis is orthonormal. Why is that?

We did the following examples.

3. Use Octave to find the QR decomposition for $A = \begin{pmatrix} 1 & 1 & 6 \\ 0 & 2 & -3 \\ -1 & 3 & 0 \end{pmatrix}$.

   A = [1 1 6; 0 2 -3; -1 3 0];
   [Q, R] = qr(A)

4. Find the QR decomposition for $B = \begin{pmatrix} 1 & 1 \\ 1 & 1 \end{pmatrix}$.

Here is a video example with a tall-skinny matrix $A$ that we did not do in class.

5. Find the QR decomposition for $A = \begin{pmatrix} 2 & 3 \\ 2 & 4 \\ 1 & 1 \end{pmatrix}$. (https://youtu.be/J41Ypt6Mftc)

Fri, Mar 6

Today we introduced the idea of floating point operations (FLOPs). Every time a computer needs to add, subtract, multiply or divide two floating point numbers, we count that as one flop. We also count every square root computation as one flop. This is a theoretical estimate of how long it takes the computer to calculate the operation.

• Workshop: Floating point operations

After we got started with that workshop, we stopped to talk about computational issues with the Gram-Schmidt algorithm. We analyzed the following Octave code to perform the Gram-Schmidt algorithm.

function Q = cgs(A)
    % Returns a matrix Q with orthonormal columns by applying 
    % the classical Gram-Schmidt algorithm to the columns of A. 
    
    [m,n] = size(A);
    Q = zeros(m,n);
    for i = 1:n
        v = A(:,i);
        for k = 1:i-1
            v = v - (Q(:,k)' * A(:,i)) * Q(:,k);
        end
        Q(:,i) = v / norm(v);
    end
end

• Example: Octave classical Gram-Schmidt algorithm

We calculated that this algorithm requires $2mn^2 + mn - \tfrac{1}{2}n^2 + \tfrac{1}{2}n$ flops for a matrix with $m$ rows and $n$ columns. Typically we only focus on the leading term, so we say that asymptotically the algorithm requires $2mn^2$ flops.

Unfortunately the Gram-Schmidt algorithm is numerically unstable. One way to show this is to start with an large ill-conditioned matrix $A$, and then compute $Q$ using the algorithm. The columns of $Q$ usually won’t be orthogonal, which is a problem. We used the Hilbert matrix with $(i,j)$ entry equal to $\tfrac{1}{i+j-1}$ to show this.

n = 3
A = hilb(n);
Q = cgs(A);
norm(Q'*Q - eye(n))

Week 9 Notes

Mon, Mar 16

Class was canceled today because of the weather. But I sent everyone this workshop to try on your own.

• Workshop: Least squares introduction

Don’t forget that you can use the SageMathCell to do Octave calculations. Also the command to get the transpose of a matrix A in Octave is A' and the inverse is inv(A).

Since I wasn’t able to explain the technique in class, here is a video with an example similar to the ones in the workshop.

• Video: https://youtu.be/-bgrezOT0VQ

Wed, Mar 18

Today we talked some more about least squares regression. We started with this example.

1. There has been a steady long term decline in the number of people killed by lightning every year in the United States. The data for the years 1950 to 2020 is shown in the Octave code below. Use Octave to solve for the coefficients of the best fit trend line $\hat{y} = b_0 + b_1 x$.

    years = 1950:2020';
    deaths = [219;248;212;145;220;181;149;180;104;183;129;149;153;165;129;149;110;88;129;131;122;122;94;124;112;124;81;116;98;87;94;87;100;93;91;85;78;99;82;75;74;73;41;43;69;85;53;42;44;46;51;44;51;43;31;38;47;46;28;34;29;26;29;23;26;28;40;16;21;20;17];
    plot(years, deaths, '.')
    title("Lightning Fatalities per Year")

In the last example we used the normal equations $X^T X \mathbf{b} = X^T \mathbf{y}$ to find $\mathbf{b}$.
Unfortunately, in regression problems, the matrix $X^T X$ tends to be very ill-conditioned, so using the normal equations to solve a least squares problem directly is usually not a good idea numerically. Instead, it is better to use the QR-decomposition $X = QR$ where $Q \in \mathbb{R}^{m \times n}$ has orthonormal columns and $R \in \mathbb{R}^{n \times n}$ is upper triangular.

2. Show that $X^T X = R^T R$.

With the QR decomposition, the normal equation becomes $$R^T R \mathbf{b} = R^T Q^T \mathbf{y}.$$ We don’t actually need to solve this equation, we just need to find $\mathbf{b}$ so that $R\mathbf{b}$ equals $Q^T \mathbf{y}$ in all of the rows where $R$ is not zero.

3. Show that $R \mathbf{b} - Q^T \mathbf{y}$ is in the nullspace of $R^T$ if and only if $R \mathbf{b}$ equals $Q^T \mathbf{y}$ in every row where $R$ has a pivot.

Linear algebra packages on computers implement this approach to solve linear regression problems quickly and with very little relative error. In Matlab/Octave you can use the backslash operator to find the least squares solution to $X \mathbf{b} \approx \mathbf{y}$. We used this to get the least squares solution for the problem above.

# Least squares solution using backslash operator
X = [ones(71, 1), years];
y = deaths;
b = X \ y

You can use least squares regression to find the best coefficients for any model, even nonlinear models, as long as the model is a linear function of the coefficients. For example, if you wanted to model daily high temperatures in Farmville, VA as a function of the day of the year (from 1 to 365), you could use a function like this:

$$\hat{y} = b_0 + b_1 x + b_2 \cos\left( \dfrac{2\pi x}{365} \right) + b_3 \sin \left( \dfrac{2\pi x}{365} \right).$$

4. Use the Octave code below to create a matrix $X$ with columns corresponding to the four terms of the formula above. Then use the backslash operator to solve for the coefficient vector $\mathbf{b}$.

    days = 1:365';
    temps = [64;64;50;53;52;59;58;41;65;49;42;42;35;32;36;50;51;39;56;54;54;35;35;59;67;45;46;46;40;40;42;39;34;51;63;69;76;71;68;63;42;43;41;37;53;62;45;41;45;38;54;34;60;47;41;63;61;63;48;54;39;54;53;48;44;42;44;43;39;63;60;58;63;74;68;57;56;52;53;56;50;56;60;59;66;57;56;65;75;74;64;50;41;74;74;66;71;78;80;74;76;76;69;67;72;60;71;83;83;73;65;67;73;83;83;82;72;74;83;62;85;86;86;83;83;75;76;79;81;80;77;73;76;66;63;71;78;84;88;92;86;80;78;84;92;88;95;85;92;92;97;84;84;84;78;77;80;87;72;73;77;81;78;76;78;76;82;88;90;86;84;88;82;78;85;90;85;87;92;88;93;93;88;91;93;92;88;87;93;86;85;89;89;91;90;95;93;93;95;92;94;96;100;90;72;82;84;91;90;95;91;93;90;88;86;91;94;84;93;88;91;92;89;91;91;91;93;83;98;93;97;94;95;92;95;85;76;75;74;79;85;85;90;92;90;90;90;94;81;86;91;92;87;89;94;97;83;82;88;92;77;79;75;79;90;95;92;86;85;94;88;93;94;79;90;96;99;83;63;74;81;66;74;75;77;78;64;76;78;64;64;66;66;57;66;65;67;70;68;74;83;72;66;67;79;57;56;59;63;70;63;66;47;46;67;71;53;38;43;50;48;48;47;54;58;55;59;42;57;59;64;59;55;57;43;44;47;56;55;55;56;48;51;49;61;49;42;38;58;58;47;56;47;40;48;45;48;52;50;55;63;61;68;65;71];
    plot(days, temps, '.')
    title("Farmville 2019 High Temperatures")